Verilog Programs Have Stream Semantics (Verilog basics 2)

First post.

This is the second (and likely last) of two posts explaining Verilog basics from a programming languages angle. In the first post, we explained how Verilog programs are pure expressions. This gives a basis for understanding not only the basic syntax of Verilog programs, but also the structure of the expressions Verilog programs capture. However, we neglected to say anything about what Verilog programs actually mean. That’s what we’ll cover here!

Goals of this post. Whereas the first post in this series aimed to give readers a basic understanding of the simplest, lowest level subset of Verilog—structural Verilog—this post aims to give readers a basic understanding of the higher level, more useful subset of Verilog called behavioral Verilog. While we will not discuss many features within behavioral Verilog, readers should come away with an understanding of the all-important always block.

Non-goals of this post. We will not cover many features of Verilog. Even in the features we cover, we will not discuss their many, many edge cases. We will not explain the difference between reg and wire. The Verilog we present here will not always be fully legal (e.g. we avoid introducing the keyword logic for conciseness, even where it’d be required.) We also elide bitwidths for conciseness. We will not cover the difference between blocking and nonblocking assignments in always blocks.

When discussing programming languages, there are often two axes that we care about: syntax and semantics. In my first post about Verilog, I discussed the interesting points of Verilog’s syntax. Syntax simply refers to how a program in the language is written—that is, what exact strings of characters constitute a legal program. Syntax also captures the structure of a program—i.e. whether the program is a tree, a directed acyclic graph (DAG), or, in Verilog’s case, a directed graph, potentially with cycles.

One thing we have not discussed, however, is the semantics or meaning of a given Verilog program—that is what this blog post will cover. In the first post, we gave a simple example of a cyclic counter circuit, and showed how the syntax of Verilog allows us to capture the cycle in the design. However, we didn’t discuss why the design works. In this post, we will explain how the design implements a counter by discussing its semantics.

First, let’s refresh ourselves on the counter design:

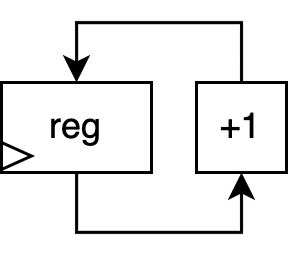
The counter consists of a register module and an incrementer module. The register holds a value. The incrementer reads that value and increments it by 1, feeding the result back into the register. The only input is the clock (indicated by the triangle input on the register) which determines when the register stores a new value, and thus, when the overall counter value is incremented.

It is easy enough to capture a cyclic design in a graphical schematic, but writing down a cycle in a programming language is more challenging. In the first post, we explained how Verilog captures cycles using placeholder wires. The result was the following implementation of our counter design:

module counter(input clk, output [7:0] out);

  wire [7:0] plusone_out, register_out;

  register register_instance(
    .in(plusone_out), .out(register_out), .clk(clk));
  plusone plusone_instance(
    .in(register_out), .out(plusone_out));

  assign out = register_out;
endmodule

Verilog implementation of our counter circuit.

We use two placeholders, plusone_out and register_out, to refer to the outputs of both modules. We then instantiate the modules, connecting inputs and outputs as indicated in the schematic.

But why does this work? To answer that, we’ll need to look at the implementations of plusone and register. Our counter implementation is written in structural Verilog—the subset of Verilog composed only of module instantiations. At the structural Verilog level, plusone and register are black boxes; we don’t actually know how they’re implemented. To understand why our counter implementation works, we’ll need to see the implementations of these submodules themselves. These implementations are written in the richer, more complex, more useful subset of Verilog called behavioral Verilog.

In the rest of this post, we will describe the implementations of plusone and register; in the process, we will cover the basics of behavioral Verilog. For each module, we will first attempt to implement the module in a software language: Python. We will then show the implementation in Verilog, and highlight the differences.

Let’s begin with the plusone module. To implement plusone in a software language like Python, you might write something like this:

def plusone(x: int) -> int:
  return x + 1

What are the semantics of this function? That is, what is its meaning? What does it do? Well, informally, the function takes a single integer x, and returns x incremented by 1.

Now let’s take a look at how we might implement our plusone module from the first post in Verilog, and see how its semantics differ from our Python implementation. To implement plusone in Verilog, we would write:

module plusone(input in, output out);
  assign out = in + 1;
endmodule

Let’s first discuss how this Verilog differs from the structural Verilog we’ve already looked at. The most important difference with our plusone module is that, in contrast to all of the Verilog we’ve seen so far, plusone actually uses an operator, +, to perform computation. This is the primary difference between behavioral and structural Verilog. Structural Verilog, as its name implies, captures the structure of a hardware design, which is simply a graph: nodes are module instantiations, and edges are wires. However, in structural Verilog, every module instantiation is a black box; a module may be named plusone, but without its implementation in behavioral Verilog, its name is just a name. Behavioral Verilog, on the other hand, provides operators (+, *, &…) and more complex features (always, initial) which allow us to specify what a module does.

Now, let’s discuss how this Verilog differs from a software language like Python. In our Verilog implementation of plusone, we simply assign the output to be the input plus one. In Verilog, this is referred to as a continuous assignment, and it indicates that the signal on the left hand side (out, in this case) will be equal to the expression on the right hand side (in+1) at all times. These words and phrases—“continuous”, “at all times”—hint that that our Verilog plusone and our Python plusone have very different meanings. Namely, there is a concept of time in the Verilog setting that doesn’t seem to exist in Python!

While we may already be starting to sense that there’s some difference between our Verilog and Python programs, our plusone example is not complex enough to make the difference clear. Let’s take a look at another example—register—which will make the difference more obvious.

Before we look at the implementations of register, let’s understand what a register is. A register (also called a “flip-flop”, or just a “flop”) is a basic unit of hardware which holds state over time. A register takes two inputs, a clock signal and an n-bit data input (often labeled D), and gives one n-bit data output (often labeled Q). A clock signal in hardware is a one-bit signal which toggles between 0 and 1 at a steady interval, synchronizing the circuit operation and indicating the passing of time. Registers are very simple: they read in a new value on the positive edge of the clock—the exact moment when the clock flips from 0 to 1—and output that value until the next positive edge. Registers are perhaps best understood by looking at an example waveform:

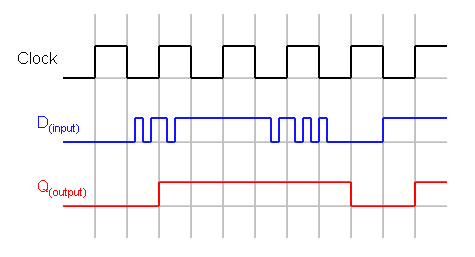
In the waveforms above, the horizontal axis is time. We see that the clock is steadily ticking between zero and one. On each positive edge of the clock (occurring on the first, third, fifth, etc. vertical gray bars) the output of the register, Q, updates to the current value of the register’s input D. Note that changes in the input D that do not occur on the positive clock edge are not reflected in the output Q. The result is that Q “holds” the previous value of D for an entire clock cycle, giving a circuit the ability to remember values from the past!

Now, let’s consider how we would implement our register module in Python. We know that a register takes two inputs, a clock and a data input, and returns a single output. So we might begin with the following function signature:

def register(clk: int, d: int) -> int:

But now, how do we implement the function? In short, a register checks whether there’s a positive edge on the clock (i.e. whether the old value is 0 and the current value is 1), and if so, returns the current data value; otherwise, it returns the old, stored data value. Sketching it out, it might look like:

def register(clk: int, d: int) -> int:
  if old(clk) == 0 and clk == 1:
    return d
  else:
    return old(d)

But what is old? Well, we’d like it to be a function that, for some input, returns the previous value of that input. But there’s a problem here—we can’t actually implement old with the information given! clk and d are simply ints—given an int, there’s no way of determining its previous value without some extra information.

How might we fix this? There are many possible ways to fix it, but they all boil down to the same solution: the register function needs more information. Perhaps the simplest way to fix our implementation is to convert clk and d into (old value, current value) tuples:

def register(clk: (int, int), d: (int, int)) -> int:
  old_clk, cur_clk = clk
  old_d, cur_d = d
  if old_clk == 0 and cur_clk == 1:
    return cur_d
  else:
    return old_d

Great! By passing in both the old value and the current value of clk and d, we now have enough information to implement the register correctly in Python. Implicitly, we made the decision to convert from scalar semantics—that is, semantics over single values—to stream semantics—that is, semantics that operate over an ordered sequence of values.

But why did this only become a problem when implementing register? That is, why were we able to implement our plusone example with scalar semantics? Well, note that plusone does not need to “look back in time”—its implementation uses data (i.e. the input in) only from the current timestep. We could pass in an (int, int) tuple for in, but we would only use its second value. (Non-essential note: this directly corresponds with the fact that, on the Verilog side, plusone is a combinational circuit; that is, its outputs are ready as soon as its inputs change.)

Now, let’s turn our attention to the Verilog implementation:

module register(input clk, 
                input d,
                output q);
  initial q = 0;
  always @ (posedge clk) q <= d;
endmodule

As with plusone, let’s first compare this behavioral Verilog to the structural Verilog we’ve seen in the past. The difference is the same as with plusone: register uses computational features of behavioral Verilog not available in structural Verilog—in this case, the initial and always keywords. We will discuss exactly what these mean in a bit.

Now, let’s compare our Verilog and Python implementations of register. Unlike our plusone example, where the Python and Verilog implementations were very similar, our register implementations look very different! The primary difference to note is that it almost seems like we’ve gone back to scalar semantics—there’s no unpacking of clk and d into “old” and “current” values. We’re able to use clk and d as values directly. However, Verilog does use stream semantics—they are just a bit more confusing. We will now elaborate.

We saw that, in Python, we needed to introduce stream semantics to implement register. That is, we needed some notion of “old” and “current”—without that, there would have been no way to capture the behavior of the register correctly. At first glance, it seems like Verilog isn’t using these stream semantics, instead treating clk, d, and q as if they were scalar values (e.g. assigning d to q rather than accessing the value of d at a specific time). Well, as it turns out, Verilog is using stream semantics—they’re just less obvious/more implicit than in our Python implementation. Instead of needing to explicitly access signal values at specific times (e.g. using old(), or using old_clk and cur_clk, as in our examples above), Verilog implicitly determines the point in time at which to access the signal, depending on the context where it is used. This is one of the most confusing elements of Verilog semantics.

Let’s take a look at a specific example. In the Python implementation of register, we determine whether there’s a positive edge on the clock in a very explicit manner:

  ...
  if old_clk == 0 and cur_clk == 1:
    ...

The equivalent line in the Verilog implementation is:

  ...
  always @ (posedge clk) ...
  ...

This is a perfect example of Verilog treating signals as streams, but implicitly. In Verilog, this is referred to as an always block, and its behavior is as you might expect: it describes events that always happen when some triggering event occurs. That triggering event is specified via a sensitivity list, “@ (...)”. In this case, our sensitivity list contains the event posedge clk, which refers to a positive edge occurring on the clk signal. Implicitly, this is treating clk as a stream; as we saw in Python, we can’t check for a positive edge when all we have is a single value. Somewhat confusingly, Verilog hides the fact that clk is a stream.

(Left as an exercise: based on the functioning of always, can you now guess what an initial block does?)

Another place where we see these implicit stream semantics are in the body of the always block:

  ...
  always @ (posedge clk) q <= d;
  ...

(Note: both q <= d and q = d are assignment statements in Verilog—nonblocking and blocking assignment, respectively. We will not discuss the difference, nor does it matter for our examples—simply read q <= d as assignment.) Though d is conceptually a sequence of values, we’re able to use it as a scalar in this assignment statement. This is because, within this always block, Verilog implicitly assumes the user wants to use the most recent value of d.

The final place where we see Verilog’s implicit treatment of streams is in the lack of an else case. In the Python implementation of register, we needed to handle the case where there was a positive edge, and the case where there wasn’t:

  ...
  if old_clk == 0 and cur_clk == 1:
    ...
  else:
    ...

However, in our Verilog implementation, we don’t see any equivalent to our else case. This is again because signals are inherently streams in Verilog. We don’t need to assign q in every case: because q is a stream, it already contains its past values, and will hold its last assigned value until the next time we run q <= d.

Finally, putting it all together, let’s take one last look at our register implementation in Verilog:

module register(input clk, 
                input d,
                output q);
  initial q = 0;
  always @ (posedge clk) q <= d;
endmodule

Recall that a register stores a value, and constantly outputs that value. On a positive clock edge, a register reads in a new value. As we’ve now seen, our always block allows us to detect when there’s a positive edge, and q <= d reads in the new value. Lastly, by taking no action on other events, the register implicitly holds the old value of q when no positive edge occurs. This covers the functioning of our register.

By putting together your understanding of the Verilog implementations of plusone and register, you should now see why counter works. If you would like to play around with an implementation of counter, see the following EDAPlayground link:

https://www.edaplayground.com/x/RKpV

To run, simply click the “Run” button. You may need to create an account first. On the right side, you’ll see the module implementations described in this post: plusone, register, and counter. On the left side, you’ll see the testbench implementation—much like a main() function in C or C++, this is the module which is actually run. Specifically, it is the initial block inside the testbench module which is run.

Surprisingly, from this very simple example of behavioral Verilog, you now have the basis for understanding most Verilog designs. The always block is at the heart of all Verilog. As soon as you understand that always blocks are simply computations that react to events, and furthermore that signals themselves are streams of values which can be reacted to, expressions like posedge clk become much more readable.

Conclusion. In this post, we explored the very basics of behavioral Verilog’s semantics. In the process, we explained how Verilog uses stream semantics, however implicitly. If you would like to continue your Verilog learning, you should now have enough knowledge to start solving Verilog challenges such as those available on https://hdlbits.01xz.net/.

One last note. Everything I’ve stated here about Verilog semantics should be taken with a grain of salt. The truth about Verilog semantics, as with any programming language, is that the semantics are defined by whatever tool is reading and processing the Verilog code. Consider the semantics assigned to the following code:

module simple();
  initial $display("Hello World");
endmodule

When run through a Verilog simulator like Verilator, which simulates a hardware design on a traditional CPU, the code will print out "Hello World" when it encounters $display("Hello World"). But simulation is just one task we might apply to a Verilog design. More likely than not, we also want to compile the design to actual hardware, be it on an FPGA or an ASIC. To do this, we use a synthesis tool, which compiles the Verilog to our hardware platform, e.g. a proprietary binary file used to program an FPGA or a low-level geometry file used to etch chips. When put through a synthesis tool like Yosys, this code will simply cause an error, as printing a message does not make sense in an actual hardware design. Thus, this single Verilog file can have two different sets of semantics based on the tool. This example is simply meant to highlight that talking about Verilog semantics can be fraught, and is entirely dependent on the tool you’re using.

Gus Smith is an alumni of the PLSE lab who recently defended his PhD. His website is located at https://justg.us.