Partial Rely—Guarantee Reasoning for Pluggable Types

Every programmer loves writing tests, but tests can’t say much about the correctness of your program. Wait a minute, what? You mean I’ve been writing tests all this time for absolutely nothing? I’ve been lied to in my undergrad software engineering course? Unfortunately, it seems like we’ve known this fact since at least 1969. A transcript from a conference on software engineering techniques sponsored by the NATO science committee contains the following quote by Edsger W. Dijkstra:

“Testing shows the absence, not the presence of bugs”

This is great! Thanks to this marvelous pearl of wisdom from 1969, it’s obvious that I should go delete all the tests I’ve ever written for all of my projects. Mike is definitely going to thank me for deleting over 64k SLOC (source lines of code) of tests from the Checker Framework. Goodbye, flaky CI pipeline! Our release process is going to go so much faster.

Alas, things aren’t that simple. Tests can be incredibly valuable, because they:

• Are executable documentation for the behaviour of a software system.
• Can give programmers confidence that a change didn’t inadvertently modify a system (e.g., regression tests).
• Can be used to generate metrics that make managers feel good¹.

So, deleting the tests in your project might be a bad idea. But let’s get back to the matter of correctness. We know tests can’t guarantee correctness, but they can document the behaviour of a software system. But what defines the behaviour of a software system, and how do we know whether that behaviour is “correct”?

It turns out, asking whether a software system is “correct” in the absence of a specification is a nonsense question. A program that crashes 50% of the time might be correct with respect to a specification that states that a program should crash 50% of the time, but completely incorrect given another specification.

So, how should programmers write a specification?

Specifications

A programmer embedded in a team with a diverse skillset (e.g., product managers, project managers, compliance engineers, etc.) might write a specification for a system by way of a design document. This document might be a plain-language description of a system, such as its intended use-cases, failure modes, and the like.

Going down a level of abstraction, source code comments (e.g., Javadoc, Python docstrings) might be written by programmers as specifications for individual components of a system, such as classes or methods. Though comments are lightweight and easy-to-read, they suffer from two related issues:

• They might drift from the actual implementation (i.e., what if a programmer updates one and not the other?).
• They are usually not machine-checked in any way.

It seems like the solution to these problems is to encode specifications directly into the system itself, making them and the program one and the same.

Types as Executable Specifications

Thinking beyond a type as that “annoying thing I have to write out every time I declare a variable in Java before they introduced the var keyword”² yields the insight that they are the closest thing programmers have seen to executable specifications. Below is some sample code:

class NonEmptyList<T> {
  List<T> backing;
  private NonEmptyList() { ... }
  public NonEmptyList(T e) { ... }
}

double avg(NonEmptyList<Integer> nel) { ... }

There are two examples of types acting as exectuable specifications here. The first is the class NonEmptyList<T>. Like the name suggests, it represents a non-empty list, and must be constructed with at least one element.

The second is the method avg, which consumes something of type NonEmptyList<Integer>. The compiler will issue a type error if a programmer ever writes code that passes in anything other than a non-empty list; presumably to remove the possibility of a divide-by-zero exception.

These types, or specifications, are type-checked by the compiler, providing a guarantee of correctness at compile-time that would have been impossible with a design document, source code comments, or other forms of specifications.

Pluggable Type Systems

The NonEmptyList<T> example in the previous section works, and is adequate for its use-case. However, it suffers from a few downsides:

• It is annoying to define an entirely new class or type for a specialization (or, refinement) of an existing type (a non-empty version of a list).
• The run-time overhead of having custom classes may not be immediately clear to programmers.

Pluggable type systems avoid these pitfalls by providing a lightweight way for programmers to pick and choose specialized types. Here is the same example as before, using a pluggable type system:

double avg(@NonEmpty List<Integer> nel) { ... }

Here, the Java basetype is List<Integer>, while the qualified type (including the pluggable type system) is @NonEmpty List<Integer>.

Using pluggable types, a programmer might even catch more bugs, or eliminate entire classes of errors entirely, all at compile-time. For example, Java’s type system is too weak to catch the error below at compile-time:

String wordInBracket = "\[.*)";
Pattern p = Pattern.compile(wordInBracket); // Run-time error!

The string “[.*)” isn’t actually a valid regular expression. However, using a pluggable type system for regular expressions, a programmer can transform this run-time error into a compile-time error:

@Regex String wordInBracket = "\[.*)"; // Compile-time error!

Unlike a custom-defined class, a pluggable type system has the advantage of all its work being done at compile-time, avoiding any run-time cost that might be incurred otherwise. In fact, some pluggable type systems, like all of those provided by the Checker Framework, generate bytecode identical to the program that does not use a pluggable type system.

Pluggable Type Systems for Possibly-Present Data

I previously stated that the standard type systems of some languages (e.g., Java) are not strong enough to catch errors at compile-time. Let’s take a look at the Java Optional type and how pluggable type systems can eliminate errors stemming from its misuse.

An instance Optional can either be present, indicating the existence of a value, or absent, meaning that there is no value. This is analogous to an object reference being non-null and null. A careful programmer might take care to check whether an Optional value is present before accessing its value:

Optional<String> optId;
...
if (optId.isPresent()) {
  optId.get();
}

Unfortunately, it is much too easy to forget this check, especially since Java’s type system does not enforce these checks at all! In fact, a programmer can simply write the following code:

optId.get();

which will throw a NoSuchElementException at run-time! Luckily, we can strengthen the Optional type with a pluggable type system to eliminate NoSuchElementExceptions entirely. Here’s the type hierarchy of the pluggable type system that we’ll use to model the Optional type:

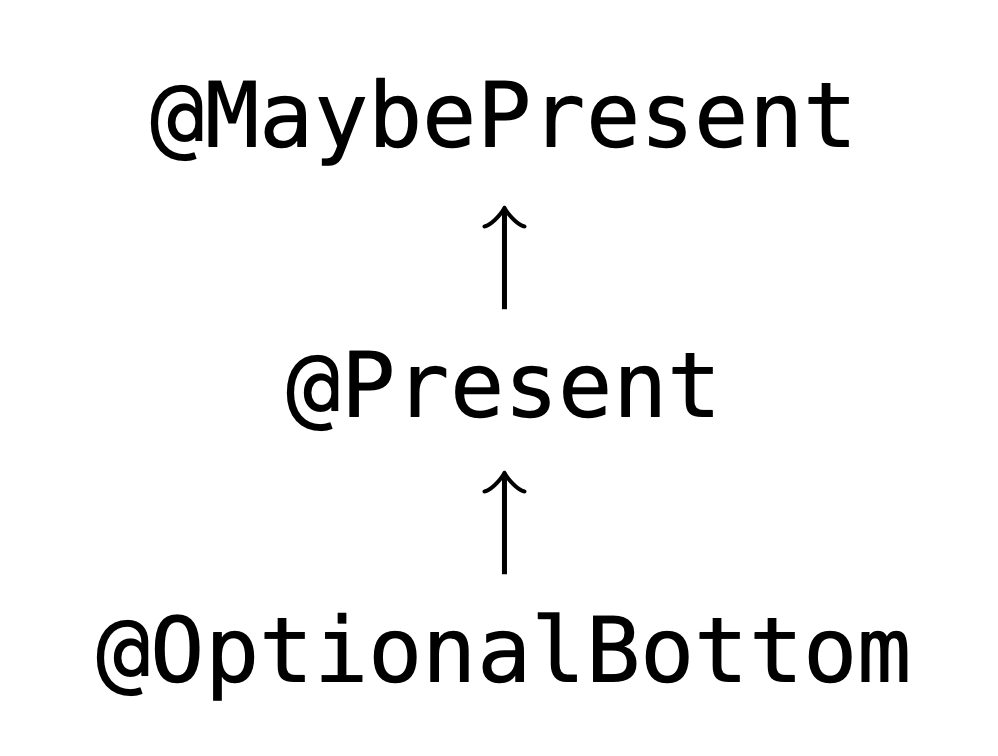
We can add the following rule to our pluggable type system:

Calls to get() on Optional values that aren’t known to be @Present are illegal

Which will enable us transform run-time NoSuchElementExceptions to compile-time errors. Here’s an example of how this rule works in-practice:

public void processId(Optional<String> optId) {
  String id = optId.get(); // Compile-time error!
  ...
}

In the code above, calling get() on optId is illegal, since there isn’t a check for whether optId is present (or not). Our pluggable type system will admit the code below, which is modified to check for optId’s presence:

public void processId(Optional<String> optId) {
  if (optId.isPresent()) {
    // optId has type @Present, here!
    String id = optId.get();
  } else {
    // optId has type @MaybePresent, here
  }
  ...
}

Great! We’ve completely eliminated NoSuchElementException from the program at run-time, right? Not exactly. How about this code?

// Invariant: nums is never empty
public int getMaxNumber(List<Integer> nums) {
  return nums.stream()
    .max(Integer::compareTo) // Produces `Optional<Integer>`
    .get();                  // Illegal under the Optional type system!
}

A programmer has documented that nums is always going to have at least one element in it, meaning that there is always going to be a maximum element. The method Stream.max returns an Optional value, which in this case will always be present. However, we cannot express this information via the Optional type system alone. Wait, I told you before that source-code comments:

// Invariant: nums is never empty

Are a terrible form of specification! Luckily, we’re experts in pluggable type systems at this point, so we can introduce a type system to express this invariant:

And now, the invariant goes from a comment to a machine-checked specification:

public int getMaxNumber(@NonEmpty List<Integer> nums) { ... }

But how should these two systems cooperate with each other?

Rely—Guarantee Reasoning for Possibly-Present Data

It’s clear that our type system for the Optional type will have to rely on the information provided by our Non-Empty type system. We can introduce special rules in our type system for operations that produce Optional values that are invoked on non-empty containers. Here is a worked example of how these rules might apply:

public int getMaxNumber(@NonEmpty List<Integer> nums) {
  return nums.stream()       // The stream is @NonEmpty
    .max(Integer::compareTo) // Max on @NonEmpty containers result in @Present Optional<T>
    .get();                  // Permissible under the Optional type system!
}

It’s clear from this example that the Optional type system needs information provided by the Non-Empty type system to precisely determine the presence of the Optional value returned from max. However, it would be foolish to rely on type information for which correctness is not guaranteed; let’s see how rely—guarantee reasoning can help us, here.

Rely—Guarantee reasoning first appeared back in the 80s as a way to verify shared-variable concurrent programs; With our reliance on the Non-Empty type system, we have eliminated the false positive we encountered with the Optional type system alone. Since the Non-Empty type system is itself machine-checked, our reliance on it is sound and the facts we establish regarding the presence of Optional values that follow from it are guaranteed. This helps us establish facts about Optional values in a program—that is—reason about the presence of Optional values that result from container operations. But, do we really need to verify all information about containers in a program?

Partial Rely—Guarantee Reasoning

If you consider what a program is at its core, it’s simply a way to manipulate data; given an input, or, some collection of inputs, produce an output (or, outputs). With this fact in mind, containers are a natural way to represent data. Lists are everywhere, in addition to other containers such as sets, maps, iterators, etc. In the context of the Optional type system (and its guarantee of no NoSuchElementException from misuse of Optional) it would be expensive and unnecessary to verify all facts about containers types.

To avoid this situation, we only need to consider the guarantee that the Optional type system and verifier provides, which is a compile-time guarantee of the absence of NoSuchElementException at run-time due to accessing an empty Optional value. We don’t guarantee anything about containers other than Optional and any errors associated with them! With this fact, we can apply a partial version of rely—guarantee reasoning, where we only care about guarantees from the Non-Empty type system that end up being used by the Optional type system.