Programming in Space and Time

While “Goto Considered Harmful” (Dijkstra, 1968) is one of the most famous pieces of writing in Computer Science, its enduring relevance to programming languages is almost wholly unappreciated or — at best — misunderstood. Historically, supporters and detractors from the original letter have addressed themselves to the conclusion that use of the goto statement should be avoided. (Including Knuth [1]) Depressingly, it took over two decades [2] before anyone bothered to empirically test Dijkstra’s claim. To the best of my knowledge, no-one ever disputed, supported, or merely considered Dijkstra’s premises and form of argument.

Dijkstra’s argument follows almost entirely from two initial remarks of a fundamentally philosophical and cognitive nature:

My first remark is that, although the programmer’s activity ends when he has constructed a correct program, the process taking place under control of his program is the true subject matter of his activity, for it is this process that has to accomplish the desired effect; it is this process that in its dynamic behavior has to satisfy the desired specifications. Yet, once the program has been made, the “making” of the corresponding process is delegated to the machine.

My second remark is that our intellectual powers are rather geared to master static relations and that our powers to visualize processes evolving in time are relatively poorly developed. For that reason we should do (as wise programmers aware of our limitations) our utmost to shorten the conceptual gap between the static program and the dynamic process, to make the correspondence between the program (spread out in text space) and the process (spread out in time) as trivial as possible.

(gendering is Dijkstra’s and archaic; bold emphasis is mine)

I will summarize these two ideas as (1) the static vs. dynamic (or space vs. time) distinction and (2) the cognitive advantage of static representations.

The former distinction — statics vs. dynamics — structures most engineering curricula that deal with physics. The latter point can be considered one of, if not the fundamental insight underlying scientific visualizations of all kinds. For example, Galileo illustrated his parabolic motion experiments with static diagrams.

left: Galileo’s notebooks; right: experimental reproduction by scientists at Rice; images from Rice

The following is from Da Vinci’s notebooks over a century earlier (but with an incorrect model of gravity) and shows the same visualization strategy.

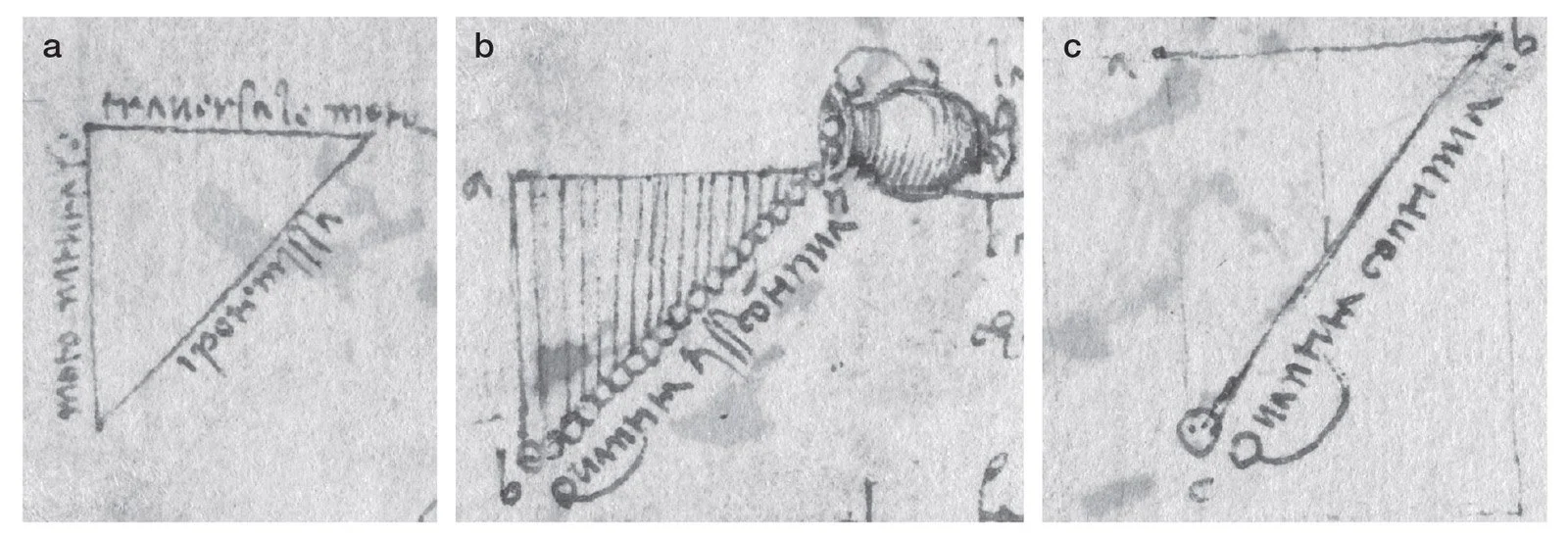Images from DaVinci’s notebooks; source: Caltech and the British Library

Both famous scientists rendered a dynamic process (“spread out in time”) into a static shape. (“spread out in space”) The apotheosis of this strategy was Decartes’ coordinates — literally co-ordinals — which allowed us to reduce geometry to arithmetic, and eventually allowed mathematicians (by analogy) to exceed the perceptual limitations of working in 2 or 3 dimensions.

After his two opening remarks, the bulk of Dijkstra’s argument consists of establishing a coordinate system for structured programs. (i.e. programs using branching, looping and such conventional control flow statements) This coordinate system identifies the dynamic process of the computation with the static, textual space of the program. To quote Dijkstra again,

Why do we need such independent coordinates? The reason is — and this seems to be inherent to sequential processes — that we can interpret the value of a variable only with respect to the progress of the process.

Dijkstra’s argument against the goto statement is that it violates the structure of this coordinate system, which is the cognitive device by which we map between our programs and their executions.

I don’t care about the goto debate any more than I care whether a colleague uses vim, emacs, or a speak-and-spell to edit documents. However, Dijkstra’s basic insight — that a program renders the temporal progress of a computational process into spatial coordinates — is profound and provocative of many more good ideas. I will highlight a few examples in the remainder of this post.

The study of parallelism and concurrency is undergirded by the problem of reasoning about time and possibility. Many seminal works draw explicit connections to physics and philosophy.

For example, Leslie Lamport has described in interviews how his familiarity with relativity and Minkowski space-time led to the development of his celebrated logical clocks [3]. In asynchronous distributed systems, just as in relativity one cannot talk about simultaneous events happening in different places. Rather, time assumes the structure of a partial ordering on events.

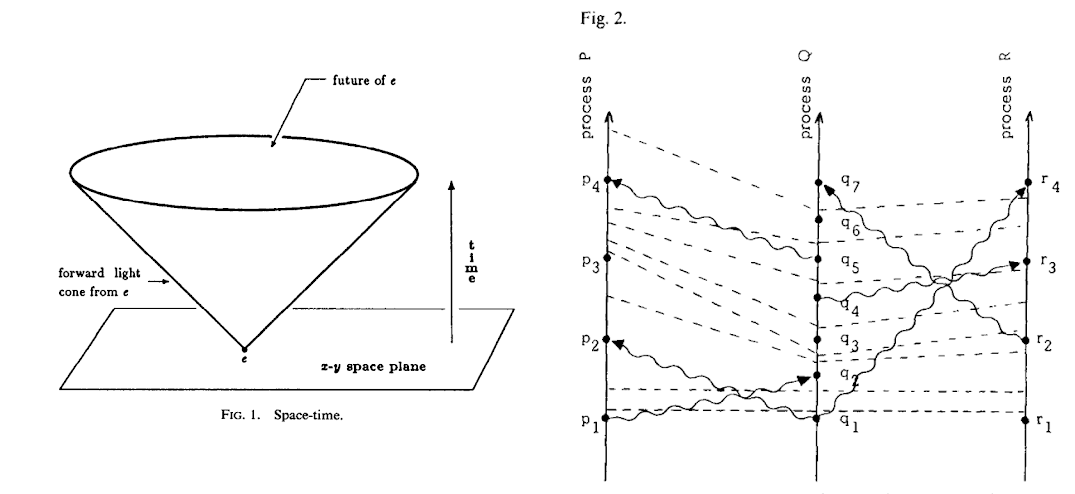left: picture of a light-cone in a 3d space-time from a 1986 paper [4] by Lamport; right: causality diagram from Lamport’s original 1978 paper [3] on clocks

On the more philosophical side, Amir Pnueli proposed a modal logic known as linear-time temporal logic (LTL) in 1977 [5]. As implied by the name, statements in LTL are concerned with properties that are necessarily true in the future. Clarke and Emerson [6] (and later Emerson and Halpern [7]) proposed alternate branching-time logics in which statements can instead be made quantifying over some or all possible futures. The logical/linguistic difference between the future vs. many futures can often be fruitfully understood with timelines and possible worlds diagrams, as you may be familiar with from popular science fiction (see below). Unfortunately, these visualizations are a long way from the sort of ideal coordinatization that Dijkstra outlined. Concurrency still makes only slightly more sense to your average programmer than time travel makes sense to your average movie watcher.

Does “Back to the Future” deserve a Turing Award for advances in temporal logic?

Recently, in collaboration with David Durst et al., I looked at the question of space-time tradeoffs in hardware design languages [8]. When designing a hardware module, there exists a fundamental tradeoff between space (i.e. how many transistors and how much die area do you use) and time (how low is the latency and high is the throughput). We reified this tradeoff into the question of whether arrays of data are spread out in space vs. spread out in time. Building on and generalizing some of these ideas, Rachit Nigam designed an HDL with timing-aware types [9]. Both works take the crucial step of expressing the logical process of the computation rather than the per-cycle transition function. Languages which require hardware designers to express programs in the latter fashion obfuscate the otherwise intuitive journey of an individual datum, through space and time.

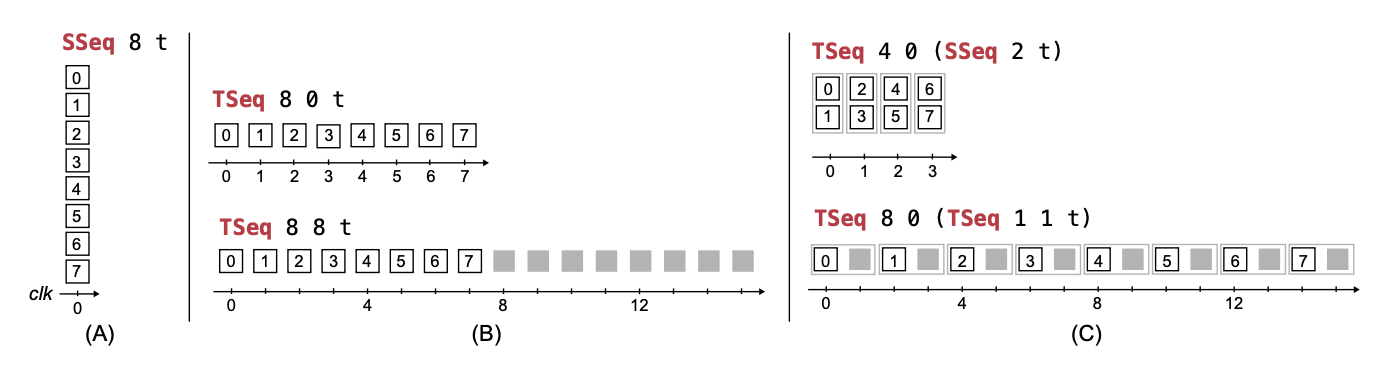(from Aetherling [8], different mappings for a sequence of 8 elements into space-time, with space depicted vertically and time depicted horizontally; grey squares mean no valid data.

To draw another connection, the above diagrams are quite reminiscent of packing problems that occur in scheduling, whether done statically by a compiler or dynamically by a processor that has direct access to the computational process unfolding in time.

I could say (and hope to say) much, much more about this topic in the future. However, I fear we are running out of both time and space in this blog post, so adieu.

---

[1] Donald E. Knuth. 1974. Structured Programming with go to Statements. ACM Comput. Surv. 6, 4 (Dec. 1974), 261–301. DOI link

[2] Barbara A. Benander, Narasimhaiah Gorla, & Alan C. Benander. 1990. An empirical study of the use of the GOTO statement. Journal of Systems and Software, Volume 11, Issue 3, 1990, Pages 217-223. DOI link

[3] Leslie Lamport. 1978. Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21, 7 (July 1978), 558–565. DOI link

[4] Leslie Lamport. 2019. The mutual exclusion problem: part I---A theory of interprocess communication. Concurrency: the Works of Leslie Lamport. Association for Computing Machinery, New York, NY, USA, 227–245. DOI link

[5] Amir Pnueli. 1977 The temporal logic of programs. 18th Annual Symposium on Foundations of Computer Science (FOCS 1977), Providence, RI, USA, 1977, pp. 46-57, DOI link

[6] Clarke, E.M., Emerson, E.A. (1982). Design and synthesis of synchronization skeletons using branching time temporal logic. In: Kozen, D. (eds) Logics of Programs. Logic of Programs 1981. Lecture Notes in Computer Science, vol 131. Springer, Berlin, Heidelberg. DOI link

[7] E. Allen Emerson and Joseph Y. Halpern. 1983. "Sometimes" and "not never" revisited: on branching versus linear time (preliminary report). In Proceedings of the 10th ACM SIGACT-SIGPLAN symposium on Principles of programming languages (POPL '83). Association for Computing Machinery, New York, NY, USA, 127–140. DOI link

[8] David Durst, Matthew Feldman, Dillon Huff, David Akeley, Ross Daly, Gilbert Louis Bernstein, Marco Patrignani, Kayvon Fatahalian, and Pat Hanrahan. 2020. Type-directed scheduling of streaming accelerators. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI 2020). Association for Computing Machinery, New York, NY, USA, 408–422. DOI link

[9] Rachit Nigam, Pedro Henrique Azevedo de Amorim, and Adrian Sampson. 2023. Modular Hardware Design with Timeline Types. Proc. ACM Program. Lang. 7, PLDI, Article 120 (June 2023), 25 pages. DOI link