Solving Concurrency Puzzles with Harmony Model Checker
Post Metadata
Despite most programming tasks today usually reasoning about concurrency at a higher abstraction level, such as transactions or managed thread pools, low-level concurrent programming maneuvers that fiddle with atomic instructions and locks never go out of fashion. In my humble opinion, the challenge of designing and debugging those programs perfectly resembles that of solving a mathematical puzzle: the description of the problem is deceivingly simple as most of them are trivial if done sequentially, but the solution that enables concurrency is often subtle, and worst, reasoning about why a solution works (or does not work) can be terribly complicated.
For prototyping and debugging this kind of concurrent programs, my Ph.D. advisor, Robbert van Renesee, and the dev team (myself included) have designed and implemented the Harmony language and the Harmony model checker over the past few years at Cornell. It started as sort of an autograder - we did not have enough TAs to manually grade all the homework for the ever-growing Operating System/Concurrent Programming class at Cornell, and the fuzzer used at that time was missing many bugs. However, 5 years later, Harmony has evolved into a full-fledged language and a highly optimized model checker, used in classes and by enterprises as well.
For time reasons, we will leave the formal theory and the design for another time. We’ll jump into action of solving puzzles!
For those who do not mind getting their hands dirty, you can follow the rest of this post by running Harmony locally yourself and try to solve those puzzles before the answers. To get the same outputs (modulo non-determinism in the generated counterexamples), you might need to compile from the source of commit 8f942f2.
Tutorial: Peterson’s Algorithm Tweaked
Peterson’s algorithm is a classic example of low-level concurrency control that ensures mutual exclusion, i.e., only one of the many threads can enter the “critical region” of the code. Without mutual exclusion, one cannot even safely increase a shared counter in the concurrent setting. Threads in Peterson’s algorithm only communicates through a shared memory and does not rely on any other synchronization primitives.
Here is an implementation of Peterson’s algorithm in Harmony. In the critical region, the threads would increase a shared counter. An assertion is put in the critical region to check mutual exclusion.
# Peterson.hny
# Suppress data race warnings
sequential flags, turn
flags = [ False, False ]
turn = choose({0, 1})
cnt = 0
def thread(tid):
while choose({ False, True }):
# Enter critical region
flags[tid] = True
turn = 1 - tid
while (flags[1 - tid]) and (turn != tid):
pass
# Critical region is here
cnt = cnt + 1
assert (cnt == 1)
cnt = cnt - 1
# Leave critical region
flags[tid] = False
spawn thread(0)
spawn thread(1)
At a high level, the two threads in Peterson’s algorithm communicate with three shared variables: a turn variable where the two thread both read and write, so there is a data race on it; and two flag variables written by one and read by the other. When both threads want to get in the critical region, the one who wins the turn data race will enterfirst. And when there is only one thread wants to enter the critical region, the corresponding flag variable will be False and allow it to enter.
As in the example code, Harmony has a Python-like syntax with the off-side rule, i.e., the code blocks are distinguished by their indentations. The only unusual feature here is choose in line while choose({ False, True }):. choose non-deterministically picks an element from the input list. In this case, it is used to model a while loop that does not necessarily terminate but always can do so.
An interesting puzzle is a tweaked version of Peterson’s algorithm below:
# PetersonTweaked.hny
...
# Enter critical region
turn = 1 - tid
flags[tid] = True
...
Lines turn = 1 - tid and flags[tid] = True are swapped. Yet, the two assignments are independent of each other. So, if everything is sequential, such a swap would not affect the behaviors of the rest of the program. But is that true in this concurrent setting?
The Harmony model checker automatically checks whether assertions hold in all possible executions. If we feed this program into the Harmony model checker, it immediately finds a counterexample that shows our tweaked version of Peterson’s algorithm can no longer guarantee mutual exclusion:
-> harmony PetersonTweaked.hny --noweb --suppress
* Phase 1: compile Harmony program to bytecode
* Phase 2: run the model checker (nworkers = 8)
* Phase 3: Scan states
* 262 states (time 0.00s, mem=0.000GB, diameter=18)
* 135/429 computations/edges
* Phase 4: Further analysis
* Phase 5: write results to PetersonTweaked.hco
* **Safety Violation**
* Phase 6: loading PetersonTweaked.hco
----------------------------------------
**Summary: something went wrong in an execution**
Here is a summary of an execution that exhibits the issue:
* Schedule thread T0: __init__()
* Line 5: Initialize flags to [ False, False ]
* Line 6: Choose 1
* Line 6: Initialize turn to 1
* Line 8: Initialize cnt to 0
* **Thread terminated**
* Schedule thread T2: thread(1)
* Line 11: Choose True
* Line 13: Set turn to 0 (was 1)
* Preempted in thread(1)
about to store True into flags[1] in line 14
* Schedule thread T1: thread(0)
* Line 11: Choose True
* Line 13: Set turn to 1 (was 0)
* Line 14: Set flags[0] to True (was False)
* Line 20: Set cnt to 1 (was 0)
* Preempted in thread(0)
about to execute atomic section in line 21
* Schedule thread T2: thread(1)
* Line 14: Set flags[1] to True (was False)
* Line 20: Set cnt to 2 (was 1)
* Line 21: Harmony assertion failed
The trace shown by Harmony says that thread T2 would first execute to line turn = 1 - tid, after which thread T1 executes both lines turn = 1 - tid and flags[tid] = True so it sets turn = 1. It enters the critical region because flag[1] is false. Then, thread T2 resumes and also enters the critical region because turn != tid is false, violating mutual exclusion.
The Harmony model checker also generates a GDB-like interactive GUI for the user to explore the counterexample.
This example illustrates the intended workflow of Harmony: 1) The user first describes the core program logic in the Harmony language; 2) The user specifies the desired program behavior — here we are using simple inline assertions, but Harmony also supports checking non-terminating states and refinement relations between a pair of Harmony programs; 3) The model checker reports no errors or an error with a counterexample and the user can iterate on the prototype program and the specification based on the feedback.
Harmony also supports black box differential testing of non-Harmony code by comparing its behaviors to those of a Harmony program’s. This can further help knowledge transfer between the Harmony prototype and the production code.
For the rest of this blog post, we will dive into four concurrency puzzles and see how they can be solved more easily (or not) with the help of Harmony.
Difficulty * : Ithaca Boat Company
Ithaca Boat Company recently implemented the following ticket booking module that can be concurrently accessed by multiple kiosks:
# ibc.hny
const NSeat = 4
sequential x
x = 0
def book() returns seat:
if x == NSeat:
seat = -1
else:
seat = x
x = x + 1
As a module intended to be called concurrently, this code has no concurrency control at all. So, it is unlikely to work as intended. But the question is, what is the worst thing that can happen?
Question 1a: Is it possible for book() in ibc.hny to return the same seat number multiple times?
Answer to Question 1a
Yes. Two threads can enter the else branch concurrently and get the same seat number.
This can be shown with the following test program in Harmony.
# ibcTest1a.hny
from ibc import *
seats = [-1, -1]
def thread(tid):
seats[tid] = book()
spawn thread(0)
spawn thread(1)
def check() returns res:
res = seats[0] != seats[1]
finally check()
It produces the following counterexample:
**Summary: something went wrong in an execution**
Here is a summary of an execution that exhibits the issue:
* Schedule thread T0: `__init__()`
* Line ibc/5: Initialize ibc$x to 0
* Line 4: Initialize seats to [ -1, -1 ]
* **Thread terminated**
* Schedule thread T1: thread(0)
* Preempted in thread(0) --> book()
about to load variable ibc$x in line ibc/12
* Schedule thread T2: thread(1)
* Line ibc/12: Set ibc$x to 1 (was 0)
* Line 7: Set seats[1] to 0 (was -1)
* **Thread terminated**
* Schedule thread T1: thread(0) --> book()
* Line ibc/12: Set ibc$x to 2 (was 1)
* Line 7: Set seats[0] to 0 (was -1)
* **Thread terminated**
* Schedule thread T3: finally()
* Line 15: Harmony assertion failed
Question 1b: Is it possible for book() in ibc.hny to return a seat number greater or equal to NSeat?
Answer to Question 1b
Yes. This might be slightly less obvious than the previous question, especially with the x != NSeat condition in place. But any number of threads can enter the else branch concurrently, which means the variable x can be increased to any integer value before some other thread returns it.
This can be shown with the following test program in Harmony.
# ibcTest1b.hny
from ibc import *
seats = [-1,] * (NSeat + 1)
def thread(tid):
seats[tid] = book()
# Harmony range is inclusive, so this creates NSeat + 1 threads
for i in {0..NSeat}:
spawn thread(i)
def check() returns res:
res = True
for i in {0..NSeat}:
res = res and (seats[i] < NSeat)
finally check()
It produces the following counterexample:
Difficulty ** : RCR Relay Race with Race Conditions
Many members of PLSE are also members of the Race Condition Running (RCR) running club. Today, they have split into teams to do a relay race.
Each team has the same number of runners. And runners on the same team take turns running legs. One arbitrary runner of each team starts, carrying a baton. When a runner of a team carrying the baton finishes their leg, they pass the team baton to another (arbitrary) runner on the same team who has not run a leg. This continues until all runners on the team have finished their legs. The teams are then ranked by the order in which the last runner finishes their leg.
(Usually, there is a fixed order of legs in relay races, but here at RCR, the order is affected by race conditions and thus not fixed.)
The following program describes RCR’s relay race, with an additional total variable that tracks the number of RCR members that have run their legs.
# RelayRace.hny
from synch import *
sequential total
const N_TEAMS = 3
const N_LEGS = 4
batons = [ Lock(), ] * N_TEAMS # lock per team
legs = [ 0, ] * N_TEAMS # counter per team
finish = Lock() # lock for the finish line
rank = [] # ranking of teams
total = 0 # total number of legs run
def runner(team):
acquire(?batons[team])
total = total + 1
legs[team] = legs[team] + 1
var last = legs[team] >= N_LEGS
release(?batons[team])
if last:
acquire(?finish)
rank += [team,]
release(?finish)
for team in { 0 .. N_TEAMS - 1 }:
for _ in { 1 .. N_LEGS }:
spawn runner(team)
This program uses locks for concurrency control, with acquire(?lock_var) and release(?lock_var) as standard lock and unlock methods of a lock.
Question 2: With 3 teams and 4 members per team, what is the set of possible values of total after all runners have finished?
Answer to Question 2
Obviously, if everything goes sequentially, then total should be 12, the total number of runners.
However, despite each team having a lock, total still has data races as it can be accessed simultaneously by runners of different teams. This hints at us that total can be 4, the number of members per team, and any value between 4 and 12 is possible.
What might be surprising is that total can be even smaller. What we need is to have total as small as possible when read by the last leg of a team. This value can be smaller by the number of members per team because a non-last leg of another team can rewrite the value. This gives us a trace that produces 2 as the final value of total:
- The first member from team A is going to write 1 into
total. - All members from team B run their legs, and the last leg of B is going to read from
total. totalbecomes 1 by the first member of team A.- The last leg of B reads 1 and is going to write 2 into
total. - All other runners finish their legs.
totalbecomes 2 by the last leg of team B.
Similarly, we can have total be 3. So, any value in [2, 12] is possible.
Another question to ask is whether total can be 1. The answer is no. Because the last write on total can only be from a last leg, and when the last leg of a team reads total, it must have been written by some runner, same team or not, which means its value is at least 1. So, the final value of total must be at least 2.
The above analysis applies to all cases where there are at least 2 teams, and each team has at least 2 members. In the degenerate case where there is only one team, the program is sequential and total can only be the number of runners on the team. In the other degenerate case where each team has only 1 runner, total can be any value from 1 to the number of teams.
One can use Harmony to find the lower bound of 2 with the following test program.
...
# same as RelayRace.hny
def check() returns res:
res = total > 2
finally check()
It produces the following (large due to 12 threads interleaving) counterexample:
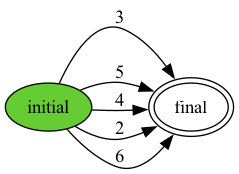
One can also use the print command of Harmony to construct a deterministic finite automata (DFA) that captures the exact set of observable behaviors produced by print to see all the possible results at once.
...
# same as RelayRace.hny except for
# const N_TEAMS = 3
# const N_LEGS = 2
# N_TEAMS = 2 and N_LEGS = 3 also runs very fast on my machine
# But N_TEAMS = 3 and N_LEGS = 3 is too slow due to DFA minimization
def main():
for team in { 0 .. N_TEAMS - 1 }:
for _ in { 1 .. N_LEGS }:
spawn runner(team)
await len(rank) == N_TEAMS
print(total)
spawn main()
Difficulty ** : One-lane Bridge
While I haven’t seen any in Seattle, several one-lane bridges exist in Ithaca. Being one-lane means all cars on the bridge can only go in one direction at a time, and the bridge must be emptied before traffic can go in the opposite direction.

The follow Harmony program models a one-lane bridge that goes from east to west. So, vehicles entering this bridge are either east bound (EB) or west bound (WB). A vehicle would first call enter(dir) with their direction and is considered on the bridge after enter(dir) returns. It will call exit(dir) sometimes afterward and is considered off the bridge when it calls exit(dir).
# onelane.hny
from synch import *
const (EB, WB) = (0, 1)
locks = [ Lock(), Lock() ]
count = 0
def enter(direction):
if direction == EB:
acquire(?locks[EB])
count += 1
if count == 1:
acquire(?locks[WB])
release(?locks[EB])
else:
acquire(?locks[WB])
def exit(direction):
if direction == EB:
acquire(?locks[EB])
count -= 1
if count == 0:
release(?locks[WB])
release(?locks[EB])
else:
release(?locks[WB])
Question 3a: Is this implementation safe such that there will never be an eastbound car and a westbound car on the bridge simultaneously?
Answer to Question 3a
Although the implementation seems only to use locks “lazily”, it is actually safe.
One can check this using Harmony by testing with some finite numbers of cars. Different from the cases above where any counterexample is sufficient for showing incorrectness, the fact that Harmony is a finite model checker means it cannot directly verify the correctness of the program for all possible numbers of cars. But testing with some finite numbers of cars would still give us some confidence in the program's correctness.
# onelaneTest1.hny
from onelane import *
cnt = [ 0, 0 ]
def car(direction):
enter(direction)
# on the bridge now
atomically: cnt[direction] += 1
assert(cnt[1 - direction] == 0)
atomically: cnt[direction] -= 1
exit(direction)
const NEB = 2
const NWB = 2
for i in { 0 .. NEB - 1 }:
spawn car(EB)
for i in { 0 .. NWB - 1 }:
spawn car(WB)
This program uses atomically to increase/decrease the counter to keep track of the number of cars in each direction on the bridge. The instructions inside an atomically block are considered atomic and are only interleaved with other instructions as a whole. This Harmony test program reports no issue.
To convince ourselves theoretically is slightly more challenging in this case. As an informal argument, if there were westbound cars on the bridge, then locks[WB] must be held by a westbound car; it is also the case that if there were eastbound cars on the bridge, then locks[WB] must be held by an eastbound car. Since locks[WB] can only be held by a single car at a time, there can be no cars in both directions on the bridge simultaneously.
Proving this more formally is also feasible and is left as an exercise for the inspired reader.
Question 3b: Is this implementation symmetric in that for any number of cars and any trace of enter(dir) and exit(dir) events produced by this implementation, this implementation would also produce another trace where the directions are flipped?
Answer to Question 3b
I feel the way this question is posed almost spoils the answer that this implementation is not symmetric.
An easy counterexample can be found by following the observation that the counter is only used by eastbound cars but not the westbound ones. While it is possible to have multiple eastbound cars on the bridge at the same time, there can be at most one westbound car on the bridge at a time because doing so requires holding locks[WB]. This implementation actually implements a reader-writer lock in a bad way (eastbound cars as readers and westbound cars as writers)!
It is easy to check this in Harmony. Using the same test program as above, assert(cnt[WB] <= 1) gives no issues, and assert(cnt[EB] <= 1) gives a concrete trace that triggers it.
However, a more interesting solution uses the behavioral refinement feature of Harmony and does not require coming up with the idea for the counterexample in the first place.
As we have seen in the previous problem, Harmony can output DFAs with print statements. So we can do that for the cars too.
# onelaneTest2a.hny
from onelane import *
cnt = [ 0, 0 ]
def car(direction):
enter(direction)
if direction == EB:
print("EB enters");
# on the bridge now
print("EB exits");
else:
print("WB enters");
# on the bridge now
print("WB exits");
exit(direction)
const NEB = 2
const NWB = 2
for i in { 0 .. NEB - 1 }:
spawn car(EB)
for i in { 0 .. NWB - 1 }:
spawn car(WB)
And it gives this DFA that one can probably tell it is not symmetric if they stare hard enough… but we would not need to do that.

We flip the EB and WB in the print statements (possibly by flipping the if condition), effectively flipping that in all behaviors. In other words, for every possible execution trace of the original program, there exists a possible execution trace of this modified program such that the only different between those two traces are that the directions are flipped.
We check this flipped program's behaviors against the DFA above for refinement. Informally, a program A's (observable) behaviors refine another program B's (observable) behaviors means that any behavior A can perform can also be performed by B. In this case, if the solution is indeed symmetric, then the set of possible behaviors should be exactly the same and the two DFAs should be equivalent. Otherwise, the refinement would not hold because some execution trace of the flipped program is impossible for the original program.
For checking behavioral refinement, we use the -B option: harmony onelaneTest2b.hny -B onelaneTest2a.hfa.
Harmony immediately reports a counterexample that some behavior in the flipped one-lane bridge is impossible in the original one. Namely, the behavior that has two westbound cars on the bridge at the same time.
**Summary: Behavior violation: unexpected output**
Here is a summary of an execution that exhibits the issue:
* Schedule thread T0: `__init__()`
* Line onelane/6: Initialize onelane$locks to [ False, False ]
* Line onelane/7: Initialize onelane$count to 0
* Line 4: Initialize cnt to [ 0, 0 ]
* **Thread terminated**
* Schedule thread T1: car(0)
* Line synch/36: Set onelane$locks[0] to True (was False)
* Line onelane/12: Set onelane$count to 1 (was 0)
* Line synch/36: Set onelane$locks[1] to True (was False)
* Line synch/41: Set onelane$locks[0] to False (was True)
* Preempted in car(0)
about to print "WB enters" in line 13
* Schedule thread T2: car(0)
* Line synch/36: Set onelane$locks[0] to True (was False)
* Line onelane/12: Set onelane$count to 2 (was 1)
* Line synch/41: Set onelane$locks[0] to False (was True)
* Line 13: Print "WB enters"
* Preempted in car(0)
about to print "WB exits" in line 15
* Schedule thread T1: car(0)
* Line 13: Print "WB enters"
* Line 13: Operation failed: Behavior failure on "WB enters"
Behavioral refinements like this are often useful when the property to be checked cannot be or is hard to express as inline assertions. Besides inline assertions and behavioral refinements, Harmony also has built-in checkers for race conditions, non-terminating states that contain deadlocks and livelocks, and active busy waiting.
Difficulty *** : Minux hackers and LSoft engineers in the same boat
According to ancient programmer folklore, Minux hackers and LSoft engineers don’t always see each other eye-to-eye due to their conflicting programming ideologies. (Or think of it as Roko’s Basilisk Followers vs. Anti-AI Luddites for the sake of 2025) It is said that a group of Minux hackers and a group of LSoft engineers happened to show up on the same ship in the ocean. And it was later found out that the ship they were sailing is a sinking one. So, they must evacuate as quickly as possible in lifeboats.
Each lifeboat can take exactly four people. However, for everyone’s safety, it can only be 4 Minux hackers, or 4 LSoft engineers, or 2 hackers and 2 engineers. Being a matter of life and death, one of the passengers on the ship hastily wrote the following program for allocating lifeboats for the two groups.
# lifeboat.hny
from synch import *
const ( MH, LE ) = ( 0, 1 )
qlock = Lock()
ninque = [ 0, 0 ]
onboard = [ Condition(), Condition() ]
def LifeBoat() : result = {
.cnt: [ 0, 0 ],
.ready: Condition(),
}
const MAXBoat = 4
boat = [ LifeBoat(), ] * MAXBoat
boatcnt = 0
def isfull(bid) returns res:
res = boat[bid].cnt[MH] + boat[bid].cnt[LE] == 4
def enqueue(ptype):
acquire(?qlock)
ninque[ptype] += 1
var boatid = -1
# if there isn't a previous person waiting for me to form a pair
# and there isn't another person to form a pair, then wait
while ((boatcnt == 0) or (boat[boatcnt - 1].cnt[ptype] % 2 == 0))
and (ninque[ptype] < 2):
wait(?onboard[ptype], ?qlock)
if (boatcnt == 0) or isfull(boatcnt - 1):
boatid = boatcnt
boatcnt += 1
else:
boatid = boatcnt - 1
ninque[ptype] -= 1
boat[boatid].cnt[ptype] += 1
if isfull(boatid):
notifyAll(?boat[boatid].ready)
notify(?onboard[ptype])
notify(?onboard[1 - ptype])
else:
if (boat[boatid].cnt[ptype] == 1)
or (boat[boatid].cnt[ptype] == 3)
or (ninque[ptype] > 1):
notify(?onboard[ptype])
else:
notify(?onboard[1 - ptype])
while not isfull(boatid):
wait(?boat[boatid].ready, ?qlock)
escape(boatid, ptype)
release(?qlock)
def escape(boatid, ptype):
if ptype == MH:
print("Minux hacker escaped on boat : ", boatid)
else:
print("LSoft engineer escaped on boat : ", boatid)
This program uses condition variables. In particular, it uses Mesa’s condition variable semantics. You can find more details in the Harmony online textbook.
This implementation’s basic idea is to get people on board the “current” boat in pairs of the same alignment. When a person is done, they will try to notify a potential next person through the condition variables.
Question 4a: Does the above solution guarantee safety, i.e., all lifeboats sent away have four people with an even number of each alignment? Does the above solution guarantee liveness, i.e., if the number of Minux hackers and the number of LSoft engineers are both even numbers and their sum is a multiple of four, do all people eventually get on board a lifeboat?
Answer to Question 4a
Perhaps unsurprisingly, the answer is no to either question.
Safety is not guaranteed because, at a high level, new calls to enqueue can interfere with the already enqueued to get on the current boat.
Liveness is not guaranteed either because once safety is broken, there can be a pair of people with different alignments at the end who cannot get on board.
Both cases can be analyzed automatically with the following Harmony program:
# lifeboatTest.hny
from lifeboat import *
def check() returns res:
res = True
for i in { 0 .. boatcnt - 1 }:
res = res and (boat[i].cnt[MH] + boat[i].cnt[LE] == 4)
and ((boat[i].cnt[MH] == 0) or (boat[i].cnt[LE] == 0)
or (boat[i].cnt[MH] == boat[i].cnt[LE]))
const NMH = 4
const NLE = 4
for i in { 0 .. NMH - 1 }:
spawn enqueue(MH)
for i in { 0 .. NLE - 1 }:
spawn enqueue(LE)
finally check()
Question 4b: Can you fix this solution to satisfy both the safety and liveness defined above (or rewrite from scratch)? What do you think about the performance of your fixed solution? How much concurrency is left there?
This is an open question, and there might not be a single best answer.
Answer to Question 4b
This is an open question, and there might not be a single best answer.
...
# same as lifeboat.hny
# while ((boatcnt == 0) or (boat[boatcnt - 1].cnt[ptype] % 2 == 0))
# The only changed line:
and ((ninque[ptype] < 2) or ((boatcnt != 0) and (boat[boatcnt - 1].cnt[1 - ptype] % 2 == 1))):
# wait(?onboard[ptype], ?qlock)
The fix provided here only changes a single line: it strengthens the condition of the onboard condition variable. Now, it would not allow a pair in progress to be interleaved with another pair of different alignments.
Regarding the performance of this fixed implementation, almost everything is forced to follow a linear order dictated by qlock due to following the high-level idea described above. It is perhaps possible to allow for more concurrency with finer-grained controls. Yet, using notify on onboard should still be better than notifyAll.
Conclusion and Future Remarks
I hope you enjoyed the intellectual exercise of thinking about the meta-structures of multiple different but related worlds introduced by concurrency! I also hope I have convinced you that Harmony can be a helpful tool for exploring those structures. As demonstrated above, Harmony is highly specialized to this domain of “low-level concurrency maneuvers”. It focuses on the model, simplifies the specification, and aims for high performance and usability. In contrast, one can also model these concurrent behaviors and model check them in a more general-purpose model checker and/or language such as Alloy or TLA+. But this potentially poses a steeper learning curve because a logic language can be very different and may require more effort from the user to build all the primitives from scratch. Harmony also utilizes more domain features for better performance. A research direction we are actively exploring is to enhance model checking with programming language techniques, such as static analysis and type systems.
A further away research challenge is to verify more complex/production-level concurrent programs. As model checkers or solvers do not scale beyond certain program size or complexity thresholds due to state explosion and theorem-proving style verification is also unpractical for programs of production scales, we will likely need some dramatic new ideas. For one thing, we have not yet found a way to formulate these problems precisely and succinctly — while the answers above can communicate the intuition within a few sentences, proving those claims formally in a theorem prover today would require at least days of effort for a verification expert if not weeks or longer.
The performance of concurrency programs is another uncharted space. When these kinds of concurrency controls are involved, even high-level intuition cannot carry us much further than obvious cases. However, this also means the potential impact of research in this direction is beyond estimate. It seems to me that we are living in an exciting time when humans have not yet mastered the power of concurrency.
Acknowledgements
All credits go to Robbert for inventing the core ideas for those problems. I merely recalled them from memories of our discussions and finally wrote down my answers.
