An Introduction to Memory Consistency Models

As a follow up to Alexandra’s recent post about speculative execution and how your mental model of a computer is probably wrong, I thought I’d follow up with another example of how our programming abstraction has drifted from the underlying hardware implementation—this time with respect to when shared memory operations are visible to another program. These specifications, called memory consistency models (also just memory models or MCMs), are unfortunately tricky to understand and are famously ambiguously specified.

What is a Memory Consistency Model?

A memory consistency model is a specification of how memory operations in a program may or may not be reordered. It is a specification at the architectural level, meaning all processor implementing this instruction set architecture (ISA) must adhere to it. I bring this up because there exists a broad spectrum of microarchitectural implementations of a given ISA that may not make use of the possible reorderings afforded to it by the specification, so whether or not you witness these behaviors is not only ISA specific, but also processor specific. To introduce the basics, let’s consider the canonical example used to illustrate the seemingly strange behaviors allowed by most memory models:

In this example, memory locations \(X\) and \(Y\) are initialized to 0. What are valid values in \(r1\) for each thread that may be returned by their respective load instructions? Viewing the result as the pair \((thread_1[r1], thread_2[r1])\), obviously \((1,1)\) is possible. If you have any experience with multithreaded programming, then you also probably know that \((0, 1)\) as well as \((1, 0)\) are both possible and represent the threads interleaving with one another. What about \((0, 0)\)? Well, that depends…and if, like most programmers, this is confusing to you then you should certainly read on!

It’s first convenient to define a partial order \(<_p\), called program order, between program statements. Informally, for two statements \(s_1\) and \(s_2\), \(s_1 <_p s_2\) if they are executed by the same thread and \(s_1\) occurs earlier in the program than \(s_2\). Note, this does not necessarily mean earlier in the program text but instead earlier in the dynamic trace of the program. In our simple example, \(Store \space Y <_p Load \space X\). However, \(Store \space Y \nless_p Load \space Y\) because they exist in different threads of control.

Now, back to our example. It seems counterintuitive that the result \((0, 0)\) is ever possible because most of us think of multithreaded programs executing with what’s called a sequentially consistent memory model. A sequentially consistent memory model specifies that all memory operations must respect the program order we just defined. Let’s define another ordering, which we will call the observer order \(<_o\). Observer order defines the ordering another program with access to the same memory observes the effects of a program issuing those effects. Sometimes, this is also called total memory order. With our program order and observer order now defined, we can define more precisely what we mean by a sequentially consistent model. For arbitrary addresses \(X\) and \(Y\), the following four rules hold:

\[\begin{align} \tag{1} Load \space X <_p Load \space Y \implies Load \space X <_o Load \space Y \end{align}\] \[\begin{align} \tag{2} Load \space X <_p Store \space Y \implies Load \space X <_o Store \space Y \end{align}\] \[\begin{align} \tag{3} Store \space X <_p Load \space Y \implies Store \space X <_o Load \space Y \end{align}\] \[\begin{align} \tag{4} Store \space X <_p Store \space Y \implies Store \space X <_o Store \space Y \end{align}\]

There is nothing particularly enlightening about sequential consistency because it just says you observe things happening in the order they actually happen. Modulo thread interleavings, this is what programmers expect. Unfortunately, most architectures do not specify a sequentially consistent model and the \((0, 0)\) result is, in fact, possible. That is, both store instructions can seemingly be completely bypassed. If you would like to verify this for yourself, John Regehr has an excellent blog post here with code that exhibits this exact behavior which you can compile and run.

Does this have anything to do with caching and cache coherence?

You may be familiar with the idea of a cache and of the levels of caching in the memory hierarchy and wondering if this is at all related. In particular, often people confuse the concept of cache coherence protocols with memory consistency models. Briefly, cache coherence protocols are a method of preventing multiple cores from copying, caching, and operating on the same data without the others knowledge leading to incorrect results. These protocols specify how the caches should communicate with one another about changes to data in the cache and ownership status of blocks of data to prevent incoherent views of memory.

This is not the same thing as a memory consistency model. A memory consistency model specifies the order with which effects to the memory system can become observable by other cores. Processors implement an MCM on top of a coherent cache system and it is very possible to have a bug-free, coherent cache, but have errors with respect to your MCM. The simplest example of how this could happen is the processor reodering memory operations before they even get to the first level cache. In the rest of this post, all cache levels and main memory are referred to together as “the memory hierarchy” since the specific caching details do not matter.

Why would anyone allow this?

If you’d like to flip your desk in frustration, I understand. I promise not all computer architects have it out for us programmers (only some). If we wanted to implement a sequentially consistent core, we would have to stall both threads and wait for the store to complete before allowing the program to execute any other memory operations. A store to a shared memory location typically involves a trip to the last level cache or main memory, which takes the same amount of time as performing 10s, if not 100s, of instructions of useful work. In short, sequential consistency is slow!

To hide some of this latency, cores buffer the stores before they have completed and allow the program to continue. This optimization is effective because instructions typically don’t have data dependencies on the result of a store instruction (except in the special case of an instruction like store conditional in RISC-V), so this unblocks the rest of the program. Future loads may have to be checked against this store buffer before being sent to the rest of the memory system in a process known as memory disambiguation, but overall this optimization allows for nice performance gains. The diagram below illustrates how this store buffer optimization works:

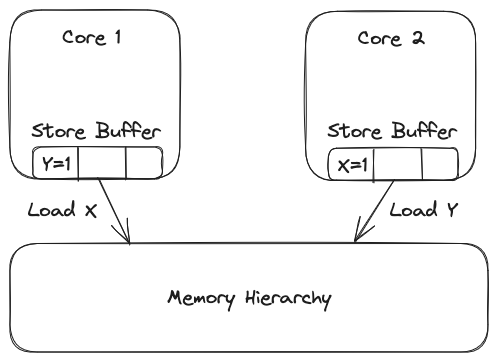
Core 1 stores to Y, but buffers this store before it completes to allow the load from address X to proceed and likewise for Core 2. Since each core does not have the data for the load they are performing in their local store buffer, the loads proceed to the memory hierarchy where they may not read the most updated value. To allow for this precise microarchitectural optimization, a weaker memory consistency model is needed.

Total Store Order

Ok, so most (all?) architectures are not sequentially consistent and that’s a pain for programmers but great for efficiency. The next weakest memory model, which is (loosely) implemented by x86, is known as total store order or TSO. It is weaker in the sense that it allows for more reorderings. TSO allows one particular reordering: loads may be lifted above stores that happen later in program order. For example, if \(Store \space X <_p Load \space Y\), the load to Y may complete before another core sees the update to X. This is precisely how you can get the counterintuitive \((0, 0)\) result discussed earlier!

One thing to note though is that the opposite effect is not true. That is, TSO does not permit a store to be reordered above a load instruction. I think these semantics are strange because it actually implies a stronger memory model than total store order, but I suppose marketing “total store and load before store order” would be challenging. To be more precise, TSO removes the equation (3) from our specification of sequential consistency above, but retains the other 3 rules:

\[\begin{align} \tag{3} \cancel{Store \space X <_p Load \space Y \implies Store \space X <_o Load \space Y} \end{align}\]

TSO also requires loads to check the store buffer on their issuing core so that if they do get reordered, program order is still kept within the thread. That is, if a thread Stores to X then Loads from X, it will see the updated value, but other cores may not! TSO weakens a sequentially consistent model just enough to allow for store buffering, no more no less. In a way, this is interesting because it reveals a specific optimization, a specific way in which our ISA abstraction fails to allow for it, and the minimal modification to permit it. Unfortunately, architectural specifications are full of these “leaked” details that have not always future-proofed so well. If, like me, you were required to learn about the MIPS branch delay slot in your undergraduate computer architecture class, then you can attest to this fact too.

An aside on x86

What I have just presented is the academic definition of TSO. Unfortunately, the most popular architecture which implements TSO (x86) has some slightly different rules because, if you can believe it, x86’s memory model was defined well after x86 was created. This actually makes sense because x86 predates multicore systems, but also has allowed for ambiguous litmus tests to define the memory model rather than a more complete specification. The research article here talks about this and develops a semantics based on observed behavior of actual processors.

Weaker Memory Models

Beyond TSO, there exists a whole spectrum of weaker consistency models in architectures like ARM, IBM Power, and RISC-V. It gets increasingly more difficult to explain and specify what each does and does not allow as the consistency models grow weaker. Some (e.g., IBM Power) do not even have a consistent “observed order” \(<_o\) property across all cores, meaning some cores can witness a different order than other cores. The spirit of most weak memory models is that if you want order use some type of fence instruction to get it. You are not, in general, guaranteed any of the four properties presented previously. RISC-V, for example, has parameterized fences that specify the type of access and the direction it’s allowed (or not allowed) to cross. For example, you could specify a fence that allows reads to cross it to happen earlier, but not cross in the other direction. Since RISC-V and ARMv8 now have largely similar memory models, I’ll explain some of the key characteristics of the RISC-V Weak Memory Ordering (RVWMO) as a representative of popular weak memory models to give you an idea of what these look like and the order they do (not) impose.

RISC-V Memory Model

The RISC-V memory model imposes a total order on all memory operations though as you may have come to expect, it is not deterministic between executions. There are 13 patterns of accesses where order must be maintained, otherwise who knows! The following diagram shows one form of ordering that’s enforced:

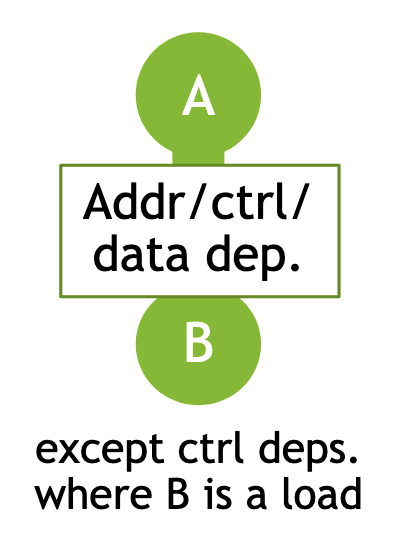
Figure from Dan Lustig’s RVWMO Presentation Slides

In the figure above, A and B represent arbitrary accesses and the white box between them gives a rule, which blocks their reordering. This rule actually represents 3 of the 13 patterns that the memory model specifies—one for each of address, control, and data dependency. So we are on the same page, here’s what those words mean:

• address dependency: Access A’s result is involved in the computation of the address for access B
• control dependency: Access A’s result determines if access B executes at all
• data dependency: Access A’s result is required in the computation of the data that access B uses (think a load then a store to the same address)

If one of these dependencies hold, then ordering is maintained with the noted exception in the figure for allowing speculative loads. These dependencies are determined by a set of syntactic rules on the program. I chose to present this rule because it shows that programs must behave somewhat sanely, even in a weak memory model architecture (which maybe provides comfort?). If you are interested, a more complete definition of the RISC-V memory model and all the rules defining the various dependencies is presented in this RISC-V developers blog post.

When will I ever need to use this?

Despite all the chaos that I have just discussed, it’s pretty likely that most readers and programmers will have never dealt with a memory-reordering bug. Most high-level languages, like C++ and Java, actually guarantee as part of a language-level memory model “sequential consistency for data-race free programs” (sometimes called SC for DRF or DRF-SC). That’s right, some languages implement a memory model on top of the underlying architecture’s memory model. To get sequential consistency, compilers insert the necessary fence instructions around synchronization operations.

Since this is the PLSE blog, here is the OCaml memory model documentation, which describes its DRF-SC implementation. All of this also means that you have to pay attention to the underlying architecture when designing a language that can express parallel computations, which I suspect may be relevant information for PL researchers.

References and Further Reading

1. The Synthesis Lectures on Computer Architecture has a volume on memory consistency here, which I referenced and found quite helpful
2. PLSE alumnus James Bornholt has a great blog post here about memory consistency models with much better diagrams
3. John Regehr’s previously linked blog post for a great practical example
4. RISC-V memory model documentation and slide deck
5. Peter Sewell, Susmit Sarkar, Scott Owens, Francesco Zappa Nardelli, and Magnus O. Myreen. 2010. X86-TSO: a rigorous and usable programmer’s model for x86 multiprocessors. Commun. ACM 53, 7 (July 2010), 89–97. https://doi.org/10.1145/1785414.1785443

Andrew Alex is a 1st year PhD student at UW, working on programming languages and computer architecture.