equivalent mutant suppression in java programs

In this post, I will relate some of the key findings and lessons learned in our 2024 ISSTA publication Equivalent Mutants In The Wild: Identifying and Efficiently Suppressing Equivalent Mutants for Java Programs (that’s a mouthful so I’ll just call it EMIW). In EMIW, my co-authors and I performed an extensive manual analysis of mutants generated for Java programs to gain insight into the types of equivalent mutants generated for real-world code. We found that a number of equivalent mutants follow simple patterns. We used these patterns to write simple, efficient static analyses, which we call suppression rules, to suppress equivalent mutants before the are ever generated. We added the suppression rules to the Major mutation framework and will refer to Major with suppression rules as EMS.

The top-line results are:

1. we gained insights into what causes mutants to be equivalent
2. we used these insights to implement EMS, an equivalent mutant suppression tool
3. we evaluated EMS and SOTA on 1.2 million mutants and found that EMS detected more than 4x as many equivalent mutants in 1/2,200th the time.

I’ll give some background on mutation analysis and then use examples of equivalent mutants to motivate our approach. Then I’ll relate our approach to previous approaches and dig into some misleading numbers.

mutation analysis

Equivalent mutants arise in mutation analysis, a technique that tries to measure how ‘good’ or adequate a test suite is. Mutation analysis begins by syntactically altering, or mutating, a program to produce a set of mutants. Typically these changes, or mutations, are small: replace + with -, a || b with a, delete a statement, etc.

Think of each mutant as an ever-so-slightly broken version of the original program that acts as a test goal. A strong test suite should detect this breakage by having at least one test that fails when run on the mutant. Any mutants that caused one or more tests to fail are killed by the test suite, and any mutants that did not cause a test failure are live. Each live mutant represents a potential shortcoming in the test suite, and these can be presented to developers to elicit new tests and incrementally improve a test suite’s quality.

example 1: improving tests with mutation analysis

Let’s step through an idealized mutation analysis workflow. Consider the program isLower:

boolean isLower(char c) {
    return c >= 'a' && c <= 'z';
}

and suppose we have an empty test suite:

class TestSuite {
    // TODO: write some tests
}

A mutation tool like Major will generate a number of mutants by performing mutations such as replacing c >= 'a' && c <= 'z' with false:

/* M1
 * < c >= 'a' && c <= 'z';
 * ---
 * > false;
 */
boolean isLower(char c) {
    return false;
}

Running our empty test suite will not kill the mutant, and the mutant’s liveness would be reported to a developer. The developer would then try write a test to kill the mutant. To do so they would need to pass inputs which cause the mutant to return a different value than the original program. You can probably do this in your head, but I find it useful to reason over truth tables:

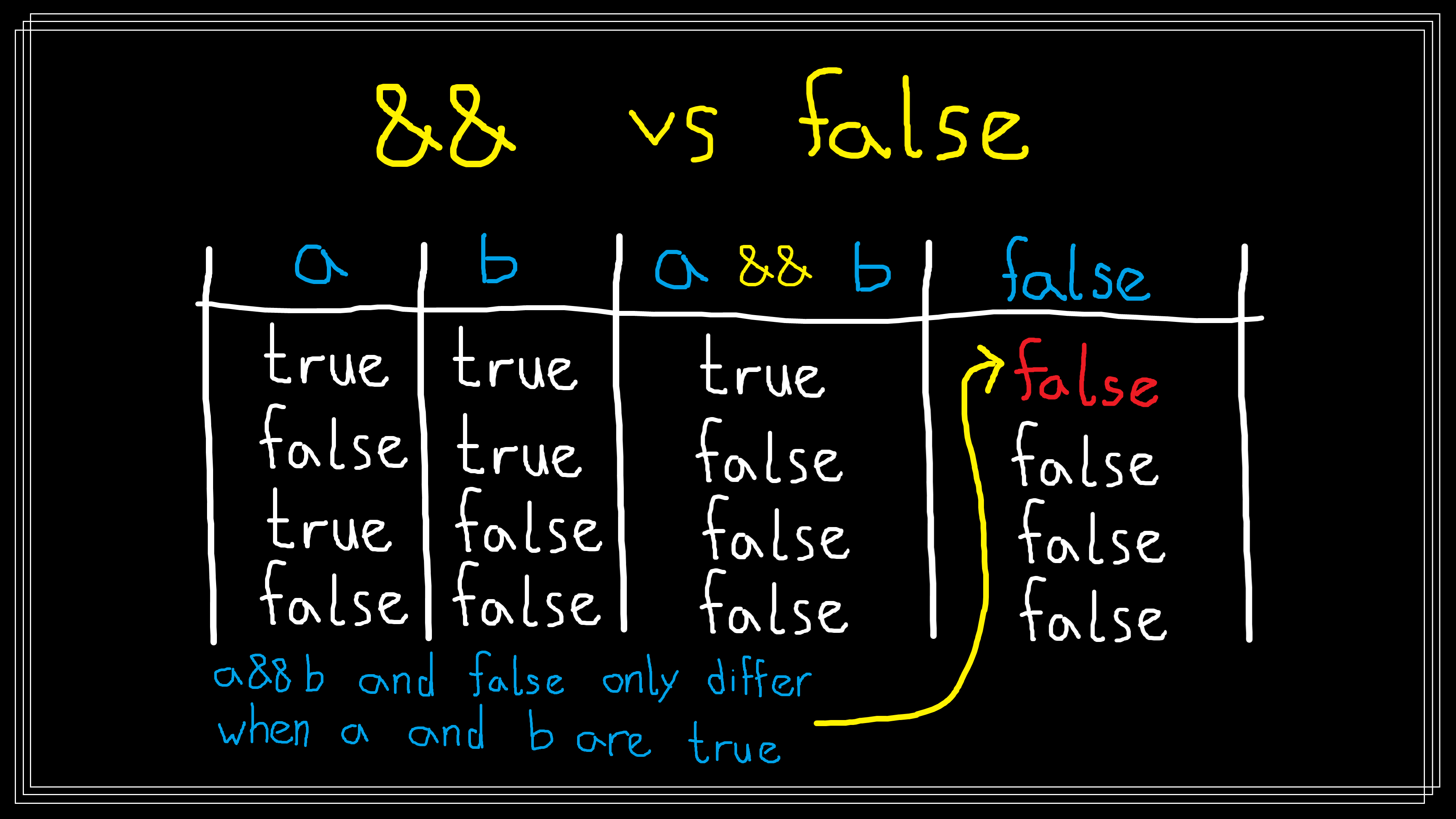
The mutant always returns false, so to kill the mutant a test must cause the original program to return true. To do so both LHS and RHS of the && operator must evaluate to true, and this implies that c must be in the range 'a' <= c <= 'z'. The developer extends their test suite with a new test:

class TestSuite {
    @Test public void testForM1(){
        assertTrue(isLower('a'));
    }
}

Running their improved test suite on the mutant leads to a test failure, and the mutant is killed.

equivalent mutants

It would be great if the story were this simple. But there’s a problem: just because we changed a program syntactically does not mean we change it semantically. Some mutants end up being semantically equivalent to the original program; we call these equivalent mutants.

Equivalent mutants are false positives of the mutation system, test goals presented to developers by the mutation system that cannot be satisfied by any test. Equivalent mutants can lead to developer frustration and lack of adoption, waste developer time, and skew metrics (e.g., mutation score, defined as the percentage of generated mutants that are killed by the test suite).

Let’s look at some examples of common forms of equivalent mutants and use these to motivate equivalent mutant suppression.

example 2: mutually exclusive equivalent mutants

Suppose we mutate && to == in isLower(char c):

/* M2
 * <     c >= 'a' && c <= 'z'
 * ---
 * >     c >= 'a' == c <= 'z'
 */
boolean isLower(char c) {
    return c >= 'a' == c <= 'z';
}

I’ll speak more about narrow mutations below, but for now it suffices to say that in general this mutation is a good one: a && b and a == b only differ when a and b are both false. When a mutant’s execution state diverges from that of the original program’s we say that the mutant has infected execution state, or just infected state. Executing a == b when either a or b is true will result in the same value as a && b and does not infect state.

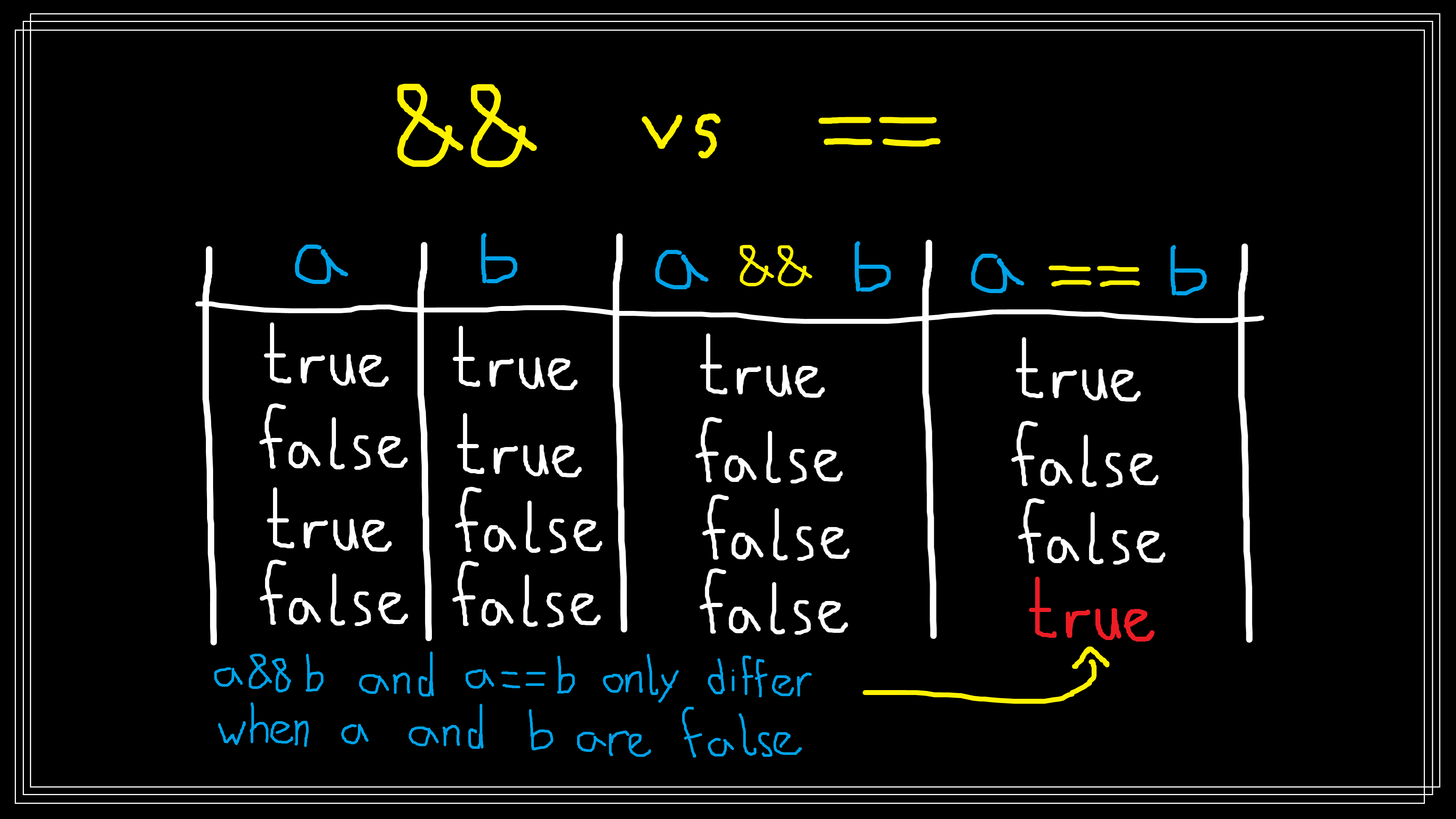
For the rest of this post, I’ll refer to the predicate required for a mutant to infect state as that mutant’s infection condition. Thus the mutation a && b \(\thickrightarrow\) a == b has an infection condition of !a && !b.

While && ⇨ == is generally an excellent mutation, it is catastrophic when applied to isLower(). For M2 to infect state it would need both c >= 'a' and c <= 'z' to be false; that is, M2’s infection condition is !(c >= 'a') && !(c <= 'z'). I’ve visualized these intervals, shown in red, in the following figure.

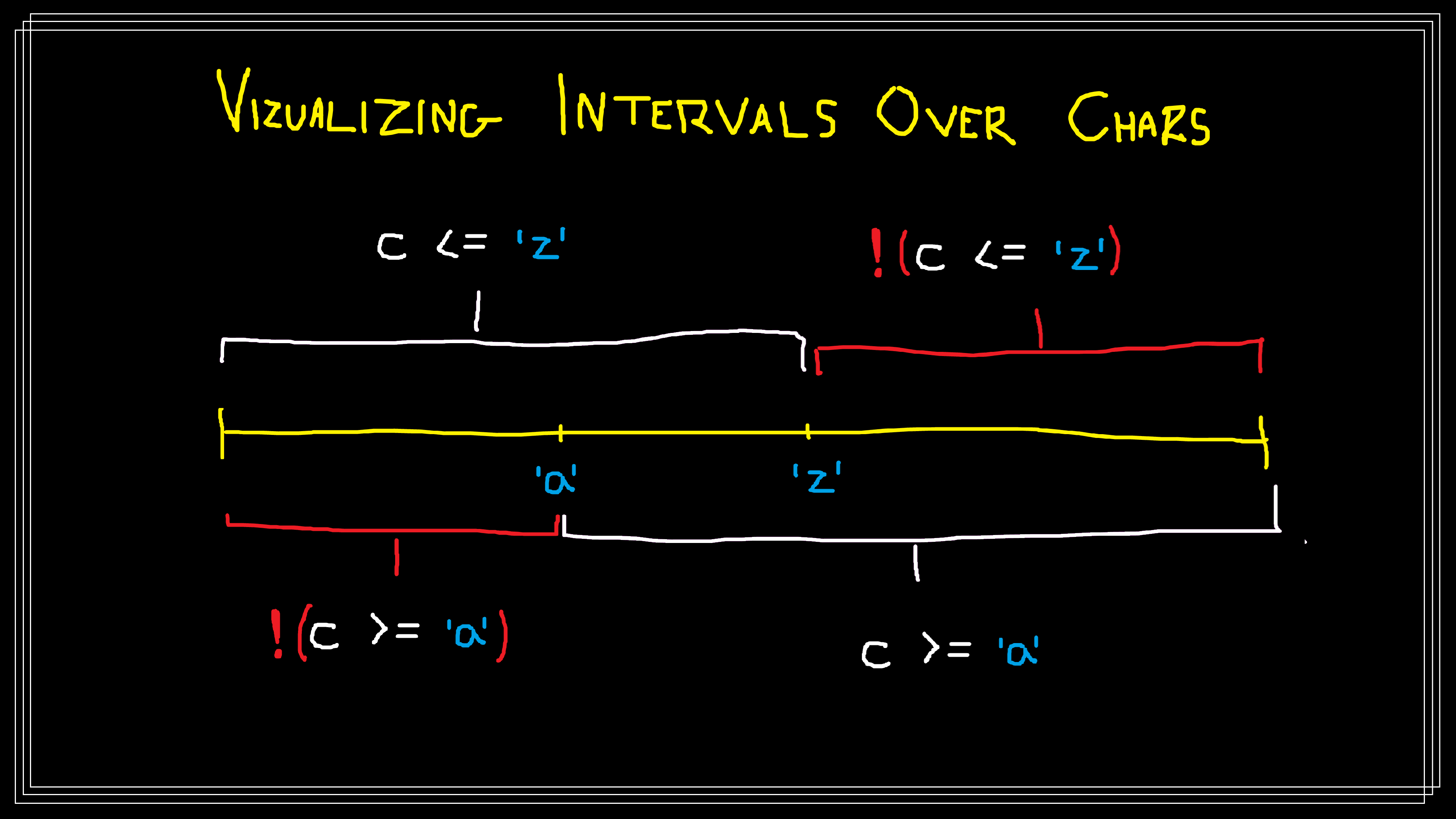This figure visualizes the relevant intervals over the char type to show that mutating c >= 'a' && c <= z to c >= 'a' == c <= 'z' results in an equivalent mutant. The yellow line represents the char type, ranging from 0 to 2^16-1. The white brackets show the intervals c <= 'z' and c >= 'a', and the adjacent red brackets show the negations of those two intervals. A value must belong to both red intervals to cause state infection, but since they are disjoint this is impossible; they are mutually exclusive.

These intervals are mutually exclusive and cannot both be occupied by c simultaneously, and thus M2 has an unsatisfiable infection condition and is an equivalent mutant.

example 3: standard library contracts

This next class of equivalent mutants is actually the class that first motivated EMS. Often times we have certain knowledge about the Java standard library that can cause a mutant to be equivalent. For instance, String.indexOf is always greater or equal to -1, Collection.size is non-negative, etc.

For instance, suppose we have a program that does a size check on a string:

if (s.length() == 0) {
    // handle empty string
}

Major will mutate s.length() == 0 to s.length() <= 0:

/* M3
 * < if (s.length() == 0) {
 * ---
 * > if (s.length() <= 0) {
 */
if (s.length() <= 0) {
    // handle empty string
}

Mutating a == b to a <= b has an infection condition of a < b: when a is greater than or equal to b the mutant and the original program will have the same evaluation. But java.lang.String lengths are non-negative and this infection condition is unsatisfiable. As in example 2, we have again created an equivalent mutant by applying a normally-good mutation in a program context where the mutation’s infection condition is unsatisfiable.

example 4: equals() reference equality check

Examples 2 and 3 showed how applying mutations in program contexts that make the mutation’s infection condition unsatisfiable leads to equivalent mutants. In this and the following example, we will show how a mutation may be applied in a context where state infection occurs but never propagates to an observable output. These types of equivalent mutants are a generally more complicated as they involve reasoning about control flow and data flow, but these two examples are relatively straightforward.

Java objects have an .equals() method used to test for object equality. It should always be true that x.equals(x), and as an optimization oftentimes a .equals() implementation will start off with a reference equality check:

class MyRecord {
    int field1;
    int field2;
    boolean field3;

    @Override
    public boolean equals(Object o) {
        if (this == o) {
            return true;
        }
        if (! (o instanceof MyRecord)) {
            return false;
        }
        return field1 == o.field1 &&
               field2 == o.field2 &&
               field3 == o.field3;
    }
}

This check avoids a number of operations such as checking if fields are equal or if o instanceof MyRecord, but doesn’t fundamentally alter the semantics of the implementation.

Major generates two mutants that skip this optimization. First, Major mutates the reference equality check to if (false) {...}, effectively skipping the shortcut for checking if the same object is equal to itself:

    /* M4
    * < if (this == o)
    * ---
    * > if (false)
    */
    if (false) {
        return true;
    }
    // ...

Second, Major will remove the return true;, replacing it with an empty statement:

    /* M5
    * < return true;
    * ---
    * > ;
    */
    if (this == o) {
        ;
    }
    // ...

In either case, removing this reference equality check will infect state: whenever executing x.equals(x) the original program will enter the then branch of the if statement and return while either mutant will continue executing the rest of the method. However, even though execution state becomes infected, this infection fails to propagate: comparing x’s fields with each other will always return true, and both the mutant and the original program return the same values.

While .equals() could technically be written so that removing this wouldn’t be an equivalent mutant (e.g., inserting a second this == 0 equality check), this would lead to some very unnatural code. Over an extensive manual analysis, every single instance of .equals() implementations we encountered that began with a reference equality check resulted in an equivalent mutant when the equality check was removed. This pattern is theoretically unsound, though we believe that if you ever write code that makes this suppression rule unsound you likely have much larger problems at hand.

example 5: useless initializations

In this final example, we show another type of equivalent mutant that successfully infects state but fails to propagate the infection to an observable output.

Consider the following pattern:

int x = 0; // a temporary initialization that is never read
if (someCond) {
    x = 1;
} else {
    x = 2;
}

In this snippet, the variable x is initialized to a temporary value of 0 and then, based on someCond, is either set to 1 or 2. This is common practice in many Java projects.

Now suppose me mutate x = 0; to x = 1;:

/* M6
 * < int x = 0;
 * ---
 * > int x = 1;
 */
int x = 1;
if (someCond) {
    x = 1;
} else {
    x = 2;
}

Unlike previous mutations, this mutant will always infect state when it executes; x will always be 1 instead of 0. However, this infected x value is never read before being overwritten, and so the infection does not propagate.

so what causes equivalent mutants?

Mutants M2 and M3 from examples 2 and 3 were equivalent due to unsatisfiable infection conditions. Mutants M4, M5, and M6 from examples 4 and 5 were equivalent due to unsatisfiable propagation conditions. Still others (not shown here) are caused by unsatisfiable reachability conditions; that is, some mutants cannot even be executed (e.g., in the then branch of if (DEBUG) { ... }).

During our manual analysis we identified a large number of repeated patterns of equivalent mutant generation. We believe there are other patterns that we have yet to identify.

equivalent mutant suppression

The predictability of the interactions that produce equivalent mutants suggests that we can detect many equivalent mutants before they are ever generated. We conducted an extensive manual analysis of 1,992 mutants to determine mutant equivalence and identify patterns of equivalence. For each pattern we extended Major with a light-weight static analysis, called a suppression rule, to identify program contexts in which a particular operator would produce an equivalent mutant. We refer to version of Major extended with suppression rules as EMS.

In total we generated 10 groups of suppression rules (some of these groups have several different similar suppression rules). Many of the patterns we found only came up a handful of times in our analysis, and it is likely that some common patterns did not show up at all in our manual analysis.

We ran Major’s mutant generation on 19 different open source Java projects, both with and without the suppression rules enabled. In total, Major was able to identify and suppress 8,776 equivalent mutants in 1.3 hours.

As a baseline we ran the state-of-the-art equivalent mutant detection system for Java programs, TCE+Soot (we describe TCE+Soot in detail in the following section). TCE+Soot detected a total of 2,124 equivalent mutants in 2,938h, taking more than 2,200x as long to find less than a quarter of the equivalent mutants found by EMS.

existing equivalent mutant detection

Prior to EMS there were broadly two approaches to equivalent mutant detection:

1. Automated reasoning, e.g. SMT solvers, to prove program equivalence.
2. Rewriting programs, e.g. with compiler optimizations, to witness program equivalence,

SMT solvers aren’t quite up to the task. While they are incredibly powerful tools, mutation analysis generates a lot of mutants, and proving program equivalence/non-equivalence can be computationally expensive.

Rewrite approaches have had more success. In 2015 Papadakis et al. introduced Trivial Compiler Equivalence (TCE). TCE is actually incredibly simple, and really kind of elegant:

1. Compile the original program with an optimizing compiler
2. Compile mutants with an optimizing compiler
3. Compare the binary outputs for equality, e.g. with diff

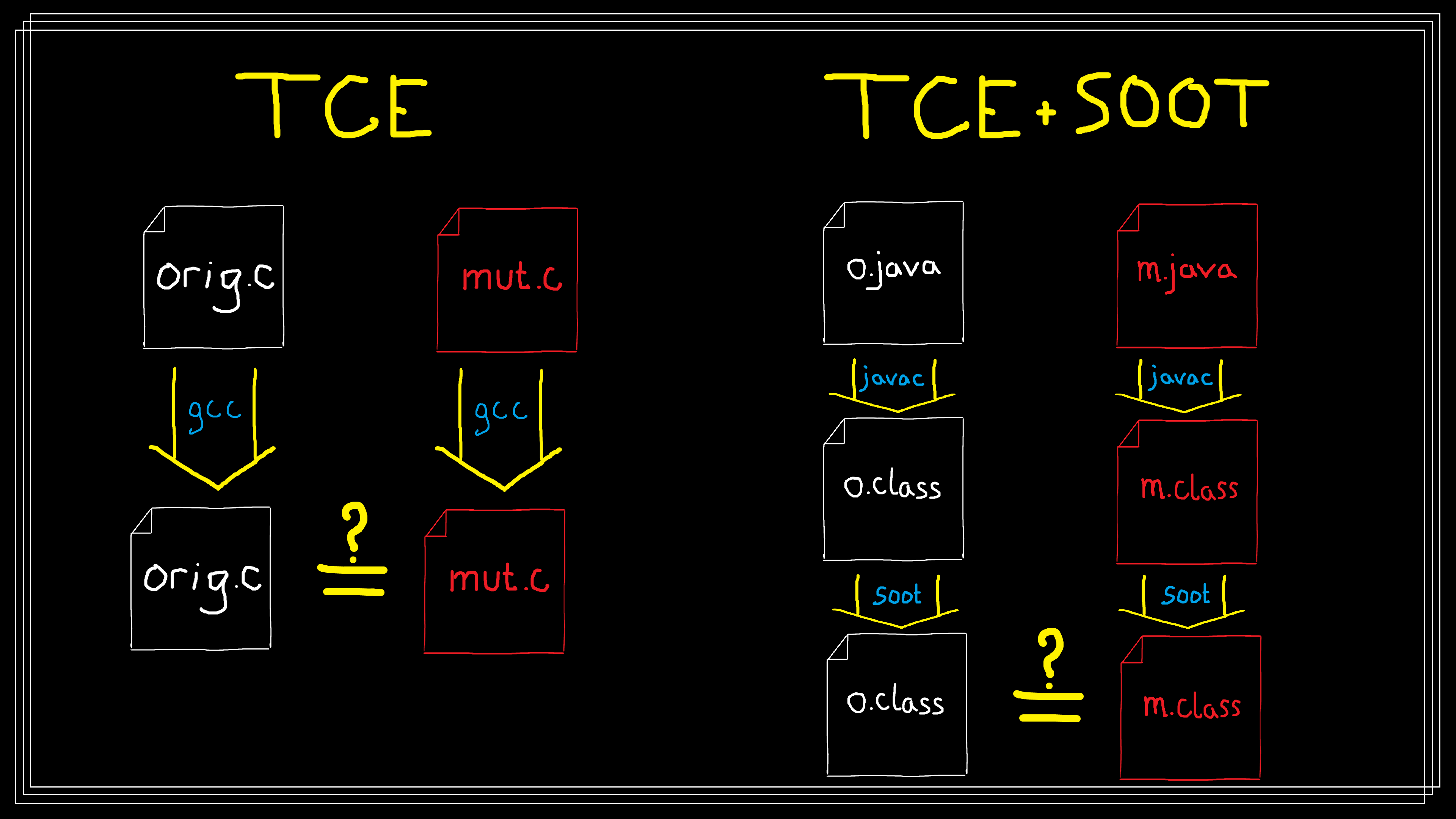
Basically, by duct taping an optimizing compiler to the diff utility, Papadakis et al. created an equivalent mutant detection system. Papadakis’ initial work used the GCC optimizing compiler for compilation.

While TCE was able to detect equivalent mutants in C programs it requires an optimizing compiler. This presents a problem for languages, like Java, that do not have an optimizing compiler. Kintis et al. attempted to address this by extending TCE to Java by using the Soot dataflow framework as a sort of post-compilation optimization pass. We’ll call this version of TCE extended with Soot TCE+Soot.

This is where the story gets tricky. TCE+Soot detected 54% of generated equivalent mutants, and this sounds great at first. However, many of the equivalent mutants were generated using a problematic mutation operator that generates a lot of equivalent mutants that TCE+Soot happens to be good at detecting. And what’s more, this is one of the only types of equivalent mutant TCE+Soot consistently detected.

For instance, replacing return x; with return x++; is equivalent because x is never read again after the post-increment is performed. In fact, 3,770 of the 3,904 (94.8%) equivalent mutants discovered to be equivalent by TCE were generated by the AOIS mutation operator (see the Discussion Section of the EMIW paper).

To our best estimates:

• AOIS accounts for 37% of the mutants generated for the TCE+Soot study, and
• If we were to remove the AOIS operator TCE+Soot would detect closer to 4% of generated equivalent mutants.

This brings up an important question: how well do equivalent mutant detection approaches generalize across different mutant generation tools? I’ll defer this to the generalizability section.

narrow mutations: a fundamental tradeoff

Another insight we had while working on this paper is that there is a fundamental tradeoff when choosing which mutants to generate. In Just et al. 2012 the authors show that certain mutations are dominated by others. For instance, consider the following mutants of a < b:

1. a != b
2. true
3. a >= b

Let’s build an infection condition table whose columns are mutants and whose rows are potential infection conditions \(a < b\), \(a = b\), and \(a > b\) for each mutant. Note that I’ll be using formatting a < b for the Java expression comparing variables a and b, and I’ll be using \(a < b\) for the mathematical predicate stating \(a\) is less than \(b\). The cell \((i,j)\) cell records if executing the \(j\)th mutant when the \(i\)th potential infection condition is true causes state to become infected.

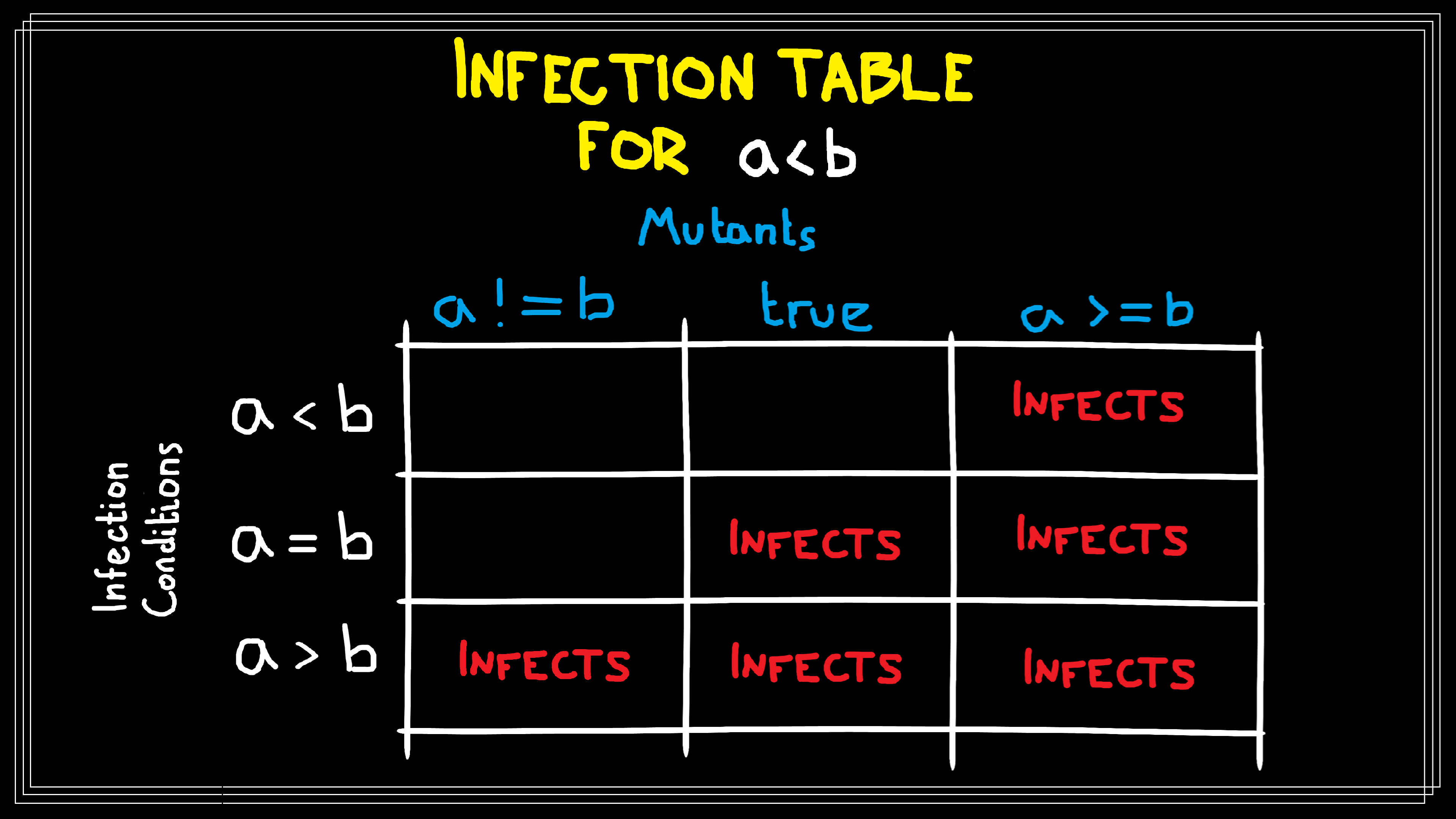
The mutant a != b only infects state when \(a > b\), mutant true infects state whenever \(a \geq b\), and mutant a >= b always infects state. Thus a != b is a narrow mutation while a >= b is a broad mutation.

Narrowness and broadness are properties about mutants’ infection conditions. If mutant \(m_1\) has infection condition \(C_1\) and mutant \(m_2\) has infection condition \(C_2\), then we say that \(m_1\) is narrower than \(m_2\) whenever \((C_1 \implies C_2) \wedge \neg(C_2 \implies C_1)\).

Narrower mutations are typically harder to detect and thus make better test goals (within reason…if a mutation is too narrow then it will not correspond to a meaningful test goal). Therefore we should prefer a != b over true, and true over a >= b.

But there is a tradeoff! While narrower mutants usually correspond to better test goals they are also are more likely to to be equivalent. For instance, if the mutant true is generated in a context where it can never infect state (and is thus equivalent), then the mutant a != b must also be equivalent. However, a != b non-infection does not imply true’s non-infection.

We also cannot infer that because a mutation frequently causes equivalent mutants it must therefore be a good mutation. The AOIS mutation technically always infects state, but often times the infection does not propagate to a observable value. When it does propagate though it will typically not be very hard to detect.

generalizability

How do we know that EMS doesn’t suffer from the same problem that TCE+Soot does? Does EMS work for mutants generated by tools other than Major? Maybe EMS’s effectiveness is just a quirk of the specific operators used by Major.

Put another way, does EMS generalize to different mutant generation techniques? We spend some time discussing this in the EMIW paper, but I’ll give a brief pitch for why our approach should generalize to other mutant generation techniques.

Our approach can generalize in two ways:

1. rule generalizability: this means the exact rules will generalize to mutants generated by other mutation systems.

2. approach generalizability: this means that another system has patterns of equivalent mutants that can be suppressed with new rules.

rule generalizability

Major mainly uses a curated subset of common mutation operators used by other mutant generation tools (e.g., µJava, PIT). Thus many of the rules used in EMS will generalize to these different systems.

Some rules do not generalize, even to other traditional systems. For instance, EMS’s mutually exclusive suppression rule (see example 2) does not apply to mutants generated by PIT. This is because PIT, which mutates Java bytecode, does not have access to high-level short-circuiting operators like && and || which have been stripped away by Javac. Therefore PIT does not produce the mutation a && b \(\Rightarrow\) a == b which is what causes the mutual exclusion equivalent mutant pattern.

However, we contend that this is not a shortcoming in EMS’s rules. Rather, this is a shortcoming in the mutants generated by PIT. As discussed in Just et al.’s 2012 paper, the mutation a && b \(\Rightarrow\) a == b is a good mutation that provides high-quality test goals.

approach generalizability

More recently there have been machine-learning based mutation systems. Broadly there are two varieties:

1. Learned mutation operators (e.g., Meta’s mutation system)
2. LLM-generated mutants (e.g., µBert, which uses CodeBERT to replace parts of code)

Some of the rules we used in EMS actually apply to both of these types of systems, but that’s not really the point of EMS. Our main point is that different mutant generation systems should have their own patterns of equivalent mutants, and by understanding these patterns we can easily suppress equivalent mutants.

The paper Comparing Mutation Testing Tools through Learning Based Mutant Selection introduces µBert by giving the following mutation:

boolean contains(Object o) {
    return indexOf(o) >= 0;
}

which is mutated to

boolean contains(Object o) {
    return lastIndexOf(o) >= 0;
}

This mutation would not be generated by traditional mutation systems and at first glance it might appear to be a desirable mutation. This seems like the type of error a developer might make in practice. But upon closer inspection this is actually an equivalent mutant. indexOf and lastIndexOf are non-negative precisely when an object is contained in the given collection.

Mutating indexOf to lastIndexOf may very well be a good mutation in many situations, but it will also generate many equivalent mutants:

• indexOf(o) > -1 or indexOf(o) == -1
• indexOf(o) when o is contained in the collection at most once

• in a context such as:

   void removeAll(Object o) {
      while (indexOf(o) > -1) {
        remove(o);
      }
   }
  

  where it doesn’t matter which order we remove elements from the collection.

conclusion and future work

We provided evidence that many equivalent mutants can be detected before they are ever generated with simple suppression rules. We used this insight to implement EMS and ran it against TCE+Soot, the current state-of-the-art equivalent mutant detection system for Java. We found that EMS detected over 4x as many equivalent mutants in less than 1/2,200th of the time.

While EMS presents solid progress on the EMP we are still a long ways away from having a full solution. Some equivalent mutants are fundamentally too difficult to be detected with simple patterns, but we believe that there are other patterns yet to be discovered. We are also interested in applying EMS to other languages to see how it compares to TCE with access to a full-fledged optimizing compiler.

EMS currently implements sound suppression rules (with the exception of the .equals() reference equality suppression rule which we described in example 4). In future work we would like to explore implementing unsound suppression rules that suppress a high proportion of equivalent mutants but possibly at the expense of some non-equivalent mutants.