Weaving Compilers

The past few weeks, I’ve been learning more about a few different kinds of weaving. One form of weaving is card weaving (also called tablet weaving), where the loom is instead replaced by square pieces of cardboard with holes punched in each corner. You may be wondering: how does a bunch of pieces of cardboard with holes weave cloth? I wondered the same thing myself! It seemed bonkers to think that you could do something with a bunch of cards that produced anything like fabric.

So, I watched a few YouTube videos, and the process seemed absolutely magical. By rotating the cards, you somehow produce cloth!

I immediately wanted to weave something using this bizarre but charmingly low-entry method, but I didn’t like a lot of the patterns I found for card weaving, so I found one for a different kind of weaving, that looks like this:

This pattern didn’t seem too complicated: 26 rows, 9 columns. Seems like it should be simple, right? Looking at the picture of this pattern, it feels like it should be obvious what the steps should be to recreate it.

However, as it turns out, it is completely un-obvious. To see why, first we’ll need to know a little more about card weaving.

Card weaving is a very old way to weave. The produced fabric, which usually consists of narrow bands, is very strong and sturdy, used for horse bridles and reins, straps for instruments, belts, etc.

As you may have seen in the videos linked above, instead of a loom, card weaving employs \(N\) cards, which are typically square in shape with holes in each corner, labeled A, B, C, and D clockwise. Each corner is threaded with a yarn. This yarn is secured and fastened on each end, on one end to a fixed object, such as a tree or doorknob, and on the other to the weaver.

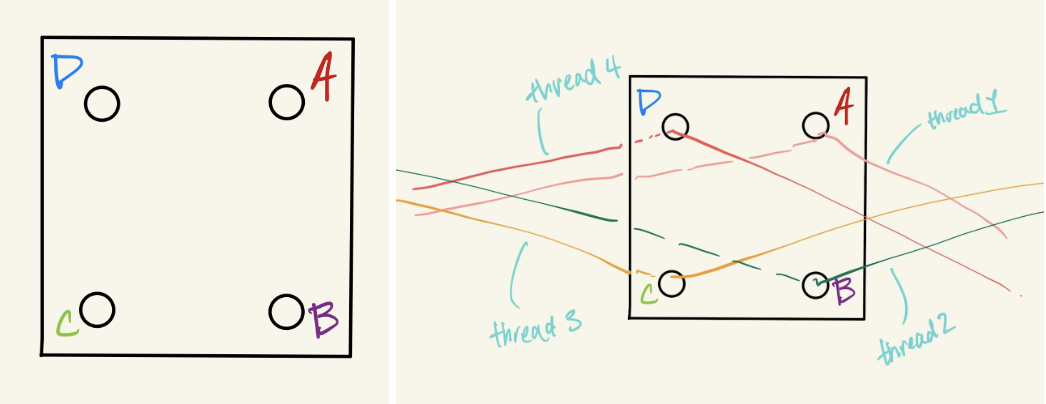
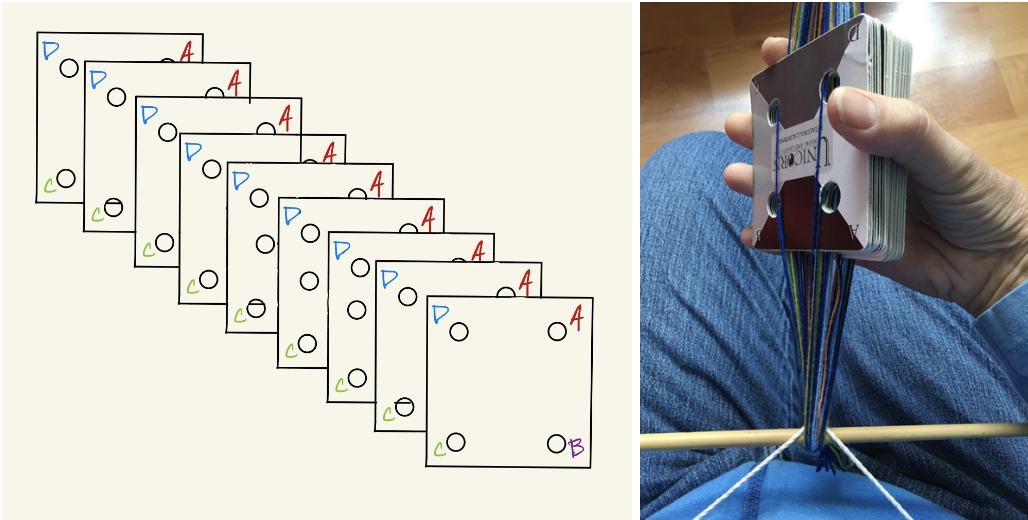
To weave, the cards are arranged so that the AD side is parallel to the ground, as shown above. A weft thread is passed above the BC threads and under the AB threads. Then, each of the N cards may be rotated “forward” or “backward”, which swaps the corners and which yarn is on top. “Forward” is a clockwise rotation of 90 degrees, resulting in the CD side being uppermost. “Backward” is a counterclockwise rotation of 90 degrees, and brings the AB side on top.

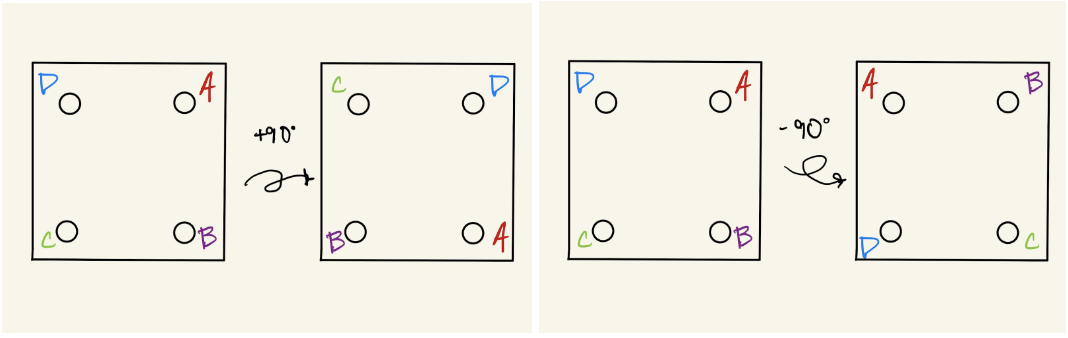
These rotations are the basic operation that gives rise to the pattern. If rotating the cards clockwise, the color in position A will be one that determines the color of the “row” you just wove. When rotating counterclockwise, it’s the color in position D.

Now that we know more about card weaving, we can reformulate our problem as follows: Given an \(M \times N\) array (\(M\) rows, \(N\) columns) where each cell contains one of \(K\) colors, can we find an assignment of colored threads to \(N\) card weaving tablets as well as \(M\) card weaving instructions such that performing the instructions on the \(N\) cards produces the pattern in the array?

For a very small \(N\), and thus a very narrow-width pattern, very small M (a very short pattern repeat), and very small number of colors \(K\), it could be feasible to find, by hand, an assignment of yarn colors to the \(4N\) holes in the cards and \(M\) operations such that the \(M\) operations on the \(N\) cards produces the pattern. However, make \(N\) or \(M\) nontrivial and it becomes quite unwieldy. One mistake could also propagate to mess up the entire rest of the pattern instructions.

For instance, can you easily come up with an assignment of threads to cards as well as clockwise/counterclockwise rotations such that the resulting weaving produces the above pattern? I can’t!

It isn’t enough to just come up with the instructions, either. A good card weaving pattern will have other “nice” properties about the amount of twist in the yarn, or a particularly intuitive progression of steps. The difficulty of coming up with a pattern from scratch combined with these factors has historically constrained how card weaving patterns are designed.

However, such a problem seems like it should be solvable with program synthesis and/or SMT solvers. While there are \(2^N\) operations that could possibly be done on N cards at any given time, this is still a finite search space, and often the cards that are used to weave the border design are only turned in one direction. This reduces the possible space to \(2^{(N - B)}\), where \(B\) is the number of border cards. Cards with only one color can be similarly ignored.

Assigning colors to holes in the cards can also be simplified using some heuristics, such as trying every set of 4 rows of the pattern as a color assignment.

While solving this problem won’t make our computers faster or more correct, it will make hundreds of patterns more accessible for people who want to get into card weaving. Card weaving is compact, flexible, and relatively cheap to get into. A pack of decent cards for card weaving costs less than $20, whereas decent looms cost at least $100, and usually quite a lot more depending on the type of loom. You could even use playing cards to DIY your own card weaving cards. For such an accessible form of weaving, it seems appropriate that designing patterns for it should be equally accessible. My proposed compiler would provide this accessibility, since it could be used to translate any array of colors into a card weaving pattern, and could be used to compile cross stitch patterns and knitting patterns in addition to patterns for other narrow bands to card weaving patterns.

I’ve barely scratched the surface here – card weaving has some other cool links to mathematics and computer science. For instance, the state of the cards (their rotation, how much twist is in the warp) is an element of an algebraic group! This isn’t just a fun fact either, it can be useful – group theory can be used to reduce the solution space using symmetry groups, as was done in the Kociemba algorithm for solving Rubik’s cubes. For another example, punch cards may be most associated today with old computers, but they were first used to encode the instructions for the Jacquard loom, and inspired the analytical engine that Ada Lovelace programmed. It feels very full-circle that computers, which were inspired by weaving machines, could be used to then help people do more weaving.