Herbie, the Numerical Compiler
Post Metadata
Ten years since its inception, the Herbie project remains an active source of research and is a marquee project of PLSE. It directly spawned four publications: Herbie at PLDI 2015, Pareto-Herbie (Pherbie) at ARITH 2021, Rival at ARITH 2023, and Odyssey at UIST 2023, and influenced many more papers (see an incomplete list). However, as with any long-standing project, we must question the fundamental idea behind it to inspire new directions of work. Previously, we pitched Herbie as a numerical analyst’s companion, a tool that automatically improves the accuracy of floating-point expressions. Now, we reenvision Herbie as a numerical compiler for programmers, lowering real expressions to floating-point implementations that are optimized for a given platform.
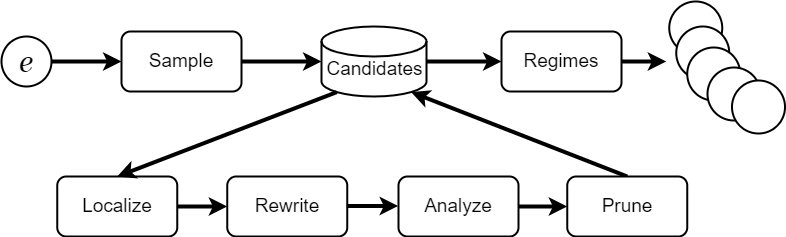
The figure above is a simplified view of Herbie.
A user provides an input expression e,
output number format,
and input number formats for each variable.
Herbie samples a set of inputs
and computes the “ground truth” outputs,
the best possible floating-point result
using real semantics via
the Rival interval library.
Herbie builds a set of candidate implementations
by iteratively applying a “generate-and-test” method
with the following steps:
- identify problematic subexpressions;
- apply rewriting strategies including rewrite rules based on mathematical identities, polynomial approximations, and more;
- analyze accuracy by comparing against ground truth values and estimate cost via a simple sum-of-operator-cost approach;
- keep only the Pareto-optimal subset of expressions.
Finally, Herbie fuses candidate implementations that individually perform well on different parts of the input domain with branch conditions, returning multiple implementations with differing accuracy versus speed tradeoffs.
Herbie, In Practice
When implementing a numerical kernel in code (or even hardware), a developer will likely start from a mathematical expression lifted from a textbook or specification. Of course, any numerical analyst would tell you to inspect the expression for sources of numerical error and rewrite the expression. Here, the developer would use Herbie to automatically apply rewrites and suggest possible alternative expressions. Based on Herbie’s output, the developer would write a final implementation in their desired platform, e.g, language, system, runtime, etc.
The process described above is not just theoretical. The primary maintainer of the project, Pavel Panchekha, used Herbie to fix bugs with complex square roots and hyperbolic trigonometry in math.js, inverse hyperbolic trigonometry in the Rust standard library, and the quadratic formula in the Racket math library.
\[\begin{array}{c} \sinh^{-1}(x) = \log(|x| + \sqrt{x^2 + 1})\\ x: \text{binary64}, \quad \sinh^{-1}(x): \text{binary64} \end{array}\] \[\Downarrow\]// Pavel's implementation from rust/rust-lang#104553
pub fn asinh(self) -> f64 {
let ax = self.abs();
let ix = 1.0 / ax;
(ax + (ax / (Self::hypot(1.0, ix) + ix))).ln_1p().copysign(self)
}
The figure above shows the Rust standard library bug in more detail. The developers of Rust naively lowered the exact formula for inverse hyperbolic sine directly to code. Unfortunately, the implementation suffers from inaccuracy for small (\(|x| < 1\)) and large values \(|x| > 10^{150}\). Using Herbie, Pavel found an implementation without inaccuracies using the special numeric functions
\[\text{log1p}(x) = \log(x) + 1, \qquad \text{hypot}(x) = \sqrt{x^2 + y^2}\]available in languages like C and Rust that are intended to increase numerical accuracy of floating-point programs. Read Pavel’s blog post for more details.
Despite these successes, any developer following the aforementioned workflow may encounter a number of limitations relevant to this blog post. Most importantly, Herbie has a fixed set of primitives it optimizes over, specifically it always uses the native OS math library. The accuracy of these primitives are based on the particular implementation in the math library and their estimated cost comes from a static table within Herbie.
Obviously, this makes little sense as the set of available primitives differ from platform to platform as well as the accuracy and relative cost of the primitives. For example, math library functions in Python have less relative variance in speed than in languages like C, lowering the performance impact of usually expensive trascendental operations. In addition, Python, notoriously, does not have a fused-multiply-add (FMA) operation, eliminating an often useful tool when implementing accurate floating-point code. As a result, being platform-agnostic or optimizing in the wrong platform may result in not-optimal accuracy versus speed tradeoffs, missing rewritings, or implementations relying on missing primitives.
The problem ultimately lies with the methodology: developers use Herbie in isolation from the target platform despite the platform having a major influence on which rewrites are most effective, the primitives that can be used, and the overall shape of an accurate implementation. The insight is that translating numerical specifications to an implementation should not consist of separate accuracy-improvement and compilation stages; this leads to a phase-ordering problem. Rather, we should extend Herbie to be platform-aware, making platform-specific decisions to implement real expressions as floating-point code.
Platforms
To allow users to specify the available primitives with their costs and implementations, we introduce a notion of platform in Herbie. Platforms are just tables of primitives with their implementations and costs. We specify platforms using a small DSL in Racket, Herbie’s implementation language, but in the future we hope to support specifying platforms in Odyssey, Herbie’s interactive frontend. Importantly, Herbie relies entirely on the platform to specify its search space and thus will only apply valid rewrites and select supported primitives in the platform.
(define avx-platform
(platform
[(binary64 binary64) (neg fabs) 1]
[(binary64 binary64) (floor sqrt round) 8]
[(binary64 binary64) sqrt 12]
[(binary64 binary64 binary64) (+ - * fmax fmin) 4]
[(binary64 binary64 binary64 binary64)
(fma fmsub fnmadd fnmsub)
4]))
Above is a prototype platform description representing AVX intrinsics for an Intel Skylake CPU. The costs are the instruction latencies from the Intel Instrincs Guide. The implementations of the primitives are specified elsewhere but in the future we would like them to also be specified here.
IRs
The two most important IRs are programs with real semantics called SpecIR, and programs with floating-point semantics called ImplIR. Up until recently, Herbie mostly rewrote ImplIR programs to other ImplIR programs and used SpecIR only in legacy subsystems like its polynomial approximator. However, we can see that compiling a mathematical specification to a floating-point implementation involves lowering a SpecIR program to a ImplIR program.
\[\begin{array}{c} f(x) = \sqrt{x + 1} - \sqrt{x},\\ \quad x: \text{binary64}, \quad f(x): \text{binary64} \end{array}\] \[\Downarrow\](- (sqrt (+ x 1)) (sqrt x)) : SpecIR
(/.f64 1 (+.f64 (sqrt.f64 (+.f64 x 1)) (sqrt.f64 x))) : ImplIR
double f(double x) {
return 1.0 / (sqrt(x + 1) + sqrt(x));
}
Interestingly,
each operator in ImplIR is just a composition of
a real mathematical operator in SpecIR and
an implicit rounding operation from a real number
to a floating-point number.
As a concrete example,
the SpecIR operator sqrt is
the usual mathematical square root,
while sqrt.f64 is the ImplIR operator
whose rounding operation maps
the real number result of sqrt
to a double-precision floating-point value.
Every ImplIR program has a unique associated SpecIR program:
the translation involves overriding the rounding operation
of every operator to the identify function.
On the other hand,
translating from SpecIR to ImplIR
requires assigning a finite-precision rounding
operation after every mathematical operation.
The initial motiviation for this change came from frustrations over maintaining Herbie’s various IRs. Some of the biggest pain points were knowing where each IR was used, correctly translating expressions between subsystem boundaries, and keeping around additional data when translation stripped important information from the expression. See a summary of these issues and a proposal to fix them. We briefly summarize some of the principles identified:
- rewrite rules based on equivalence over the reals should be applied to programs with real semantics,
- floating-point operator selection is precision tuning,
e.g., choosing to approximate
sqrtviasqrt.f64fixes the particular rounding function and number format of the result.
Thus,
Herbie’s mainloop rewrites SpecIR programs to ImplIR programs by
(1) applying rewrite rules based on
mathematical identities over SpecIR programs;
(2) applying rewrite rules that map SpecIR tiles to
a single ImplIR function application, e.g.,
(+ (* a b) c) -> (fma.f64 a b c)
(this is the actual lowering phase).
Egraphs
As with a number of projects in PLSE,
Herbie uses the egg
library for applying rewrite rules.
The multi-phased rewriting approach
described above had a number of implications
for Herbie’s use of egg.
First,
the egraph now maintains equivalence of
expressions according to real semantics, that is,
(sqrt x), (sqrt.f64 x), and (sqrt.f32 x)
will be in the same equivalence class (“eclass”) despite not
having the same numerical behavior.
Previously,
nodes within an eclass had
to also have the same output type.
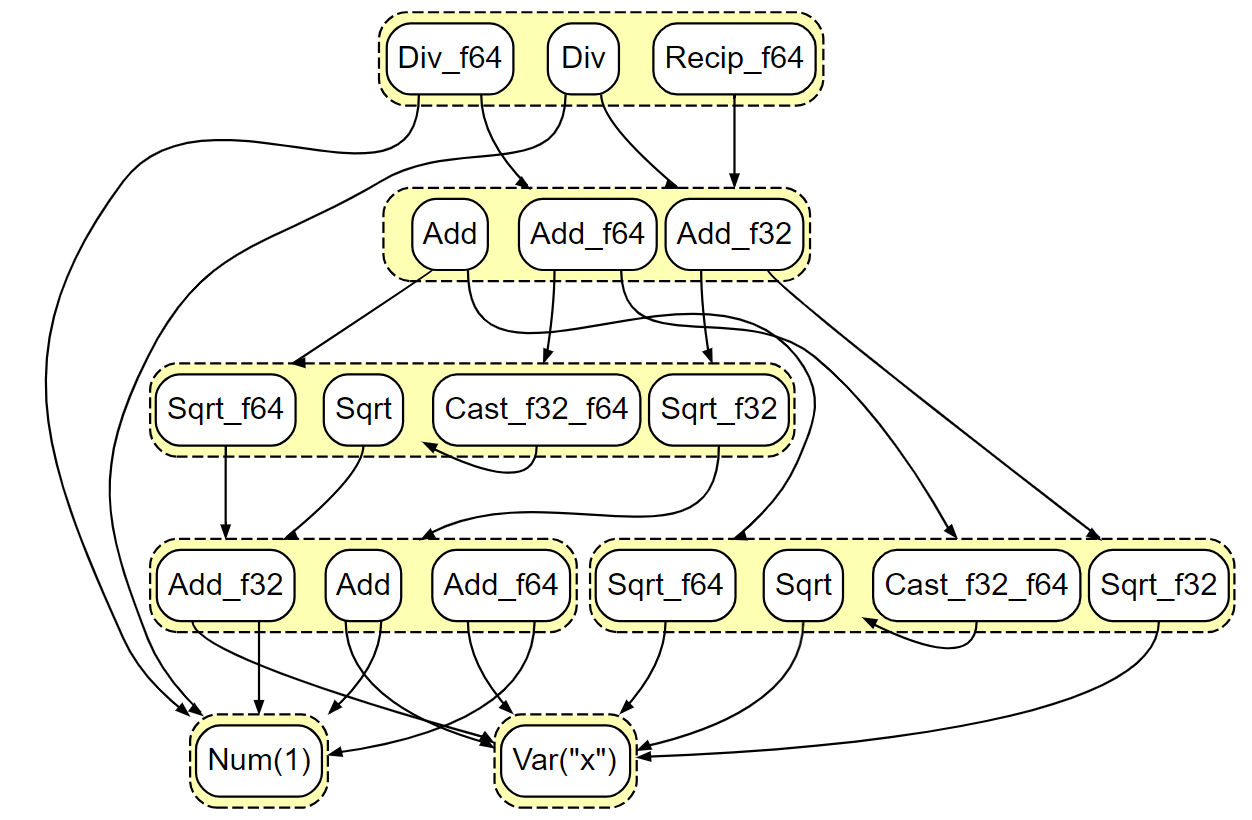
As a result,
we require typed extraction to always extract
well-typed programs from the egraph, that is,
extraction should never produce (sqrt.f64 (+.f32 x 1)).
Rather than computing
the best node for each eclass,
the extractor computes the best well-typed node
for each possibly output type.
Having no extractable type
for a given eclass represents
a failure to lower the real operator
to an actual floating-point operator,
an event that may be common in
heavily constrained platforms.
With typed extraction, we can apply the usual class of cost function that egg supports and produce a well-typed expression. It is still unclear what cost functions would help best explore the search space. The obvious cost function would utilize the per-operator platform costs to find the cheapest program in the platform. We have also considered extracting the nodes with the lowest numerical error over the sample inputs points. Perhaps, some combination of these functions would prove interesting.
Conclusion
Our new perspective on Herbie is the tool should be reframed as a platform-aware compiler that translates real expressions to floating-point implementations. To support this vision, we introduce platforms within Herbie to flexibly specify the output language to optimize over, and adapt Herbie to rewrite from programs over reals to programs over floating-point values. We believe that implementing this vision will allow users to target different platforms, produce better accuracy versus speed tradeoffs, and optimize for novel floating-point operators. Ultimately, we are excited to see what work that this new direction inspires.
Acknowledgements
Some inspiration for this new perspective arose from discussions and support under the DOE XStack project led by Hal Finkel and ASCR.
